Adding additive random noise and improved monitorization graphs

2 minute read

INTRODUCTION

After implementing the dqn refined solution in which we can try several complexities of cartpole problem, we will try to make the agent as stable as possible.

RANDOM PERTURBATIONS

The first step is to get the threshold from which our agent is not able to recover using different perturbation frequencies and perturbation intensities standard deviation.

RANDOM PERTURBATION PRELIMINARY ANALYSIS:

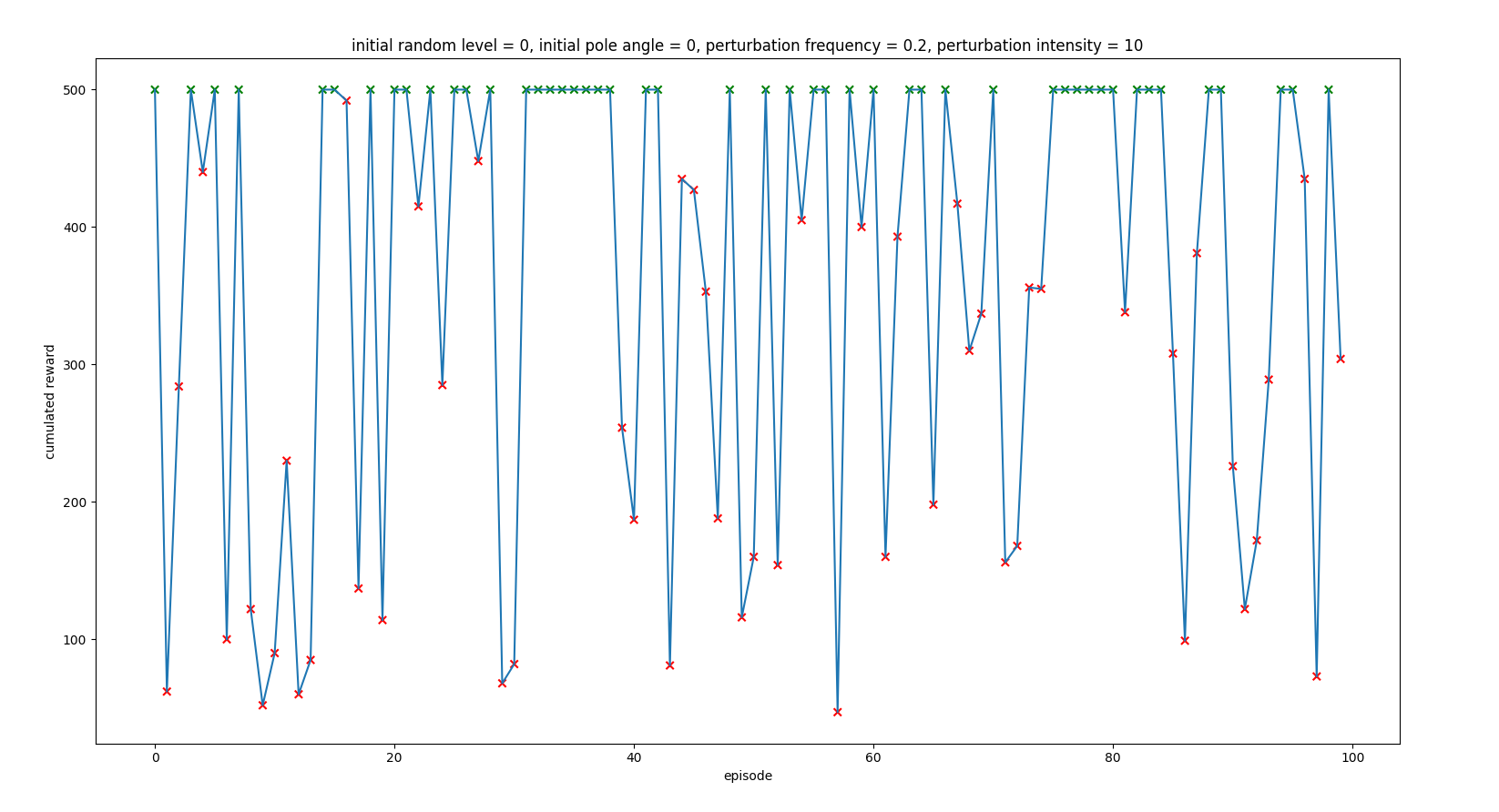
The following results are conducted with an agent trained with no perturbations

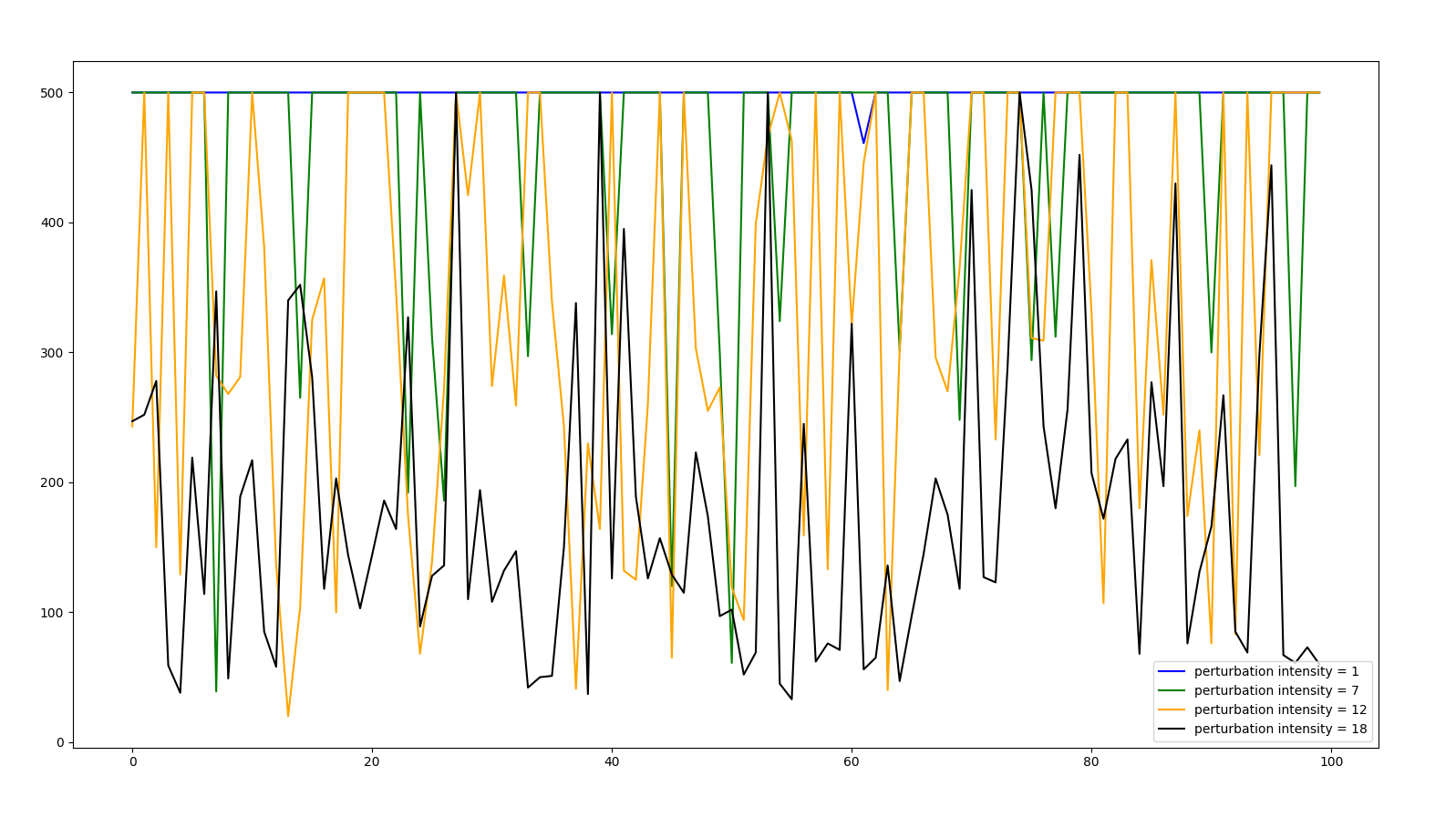
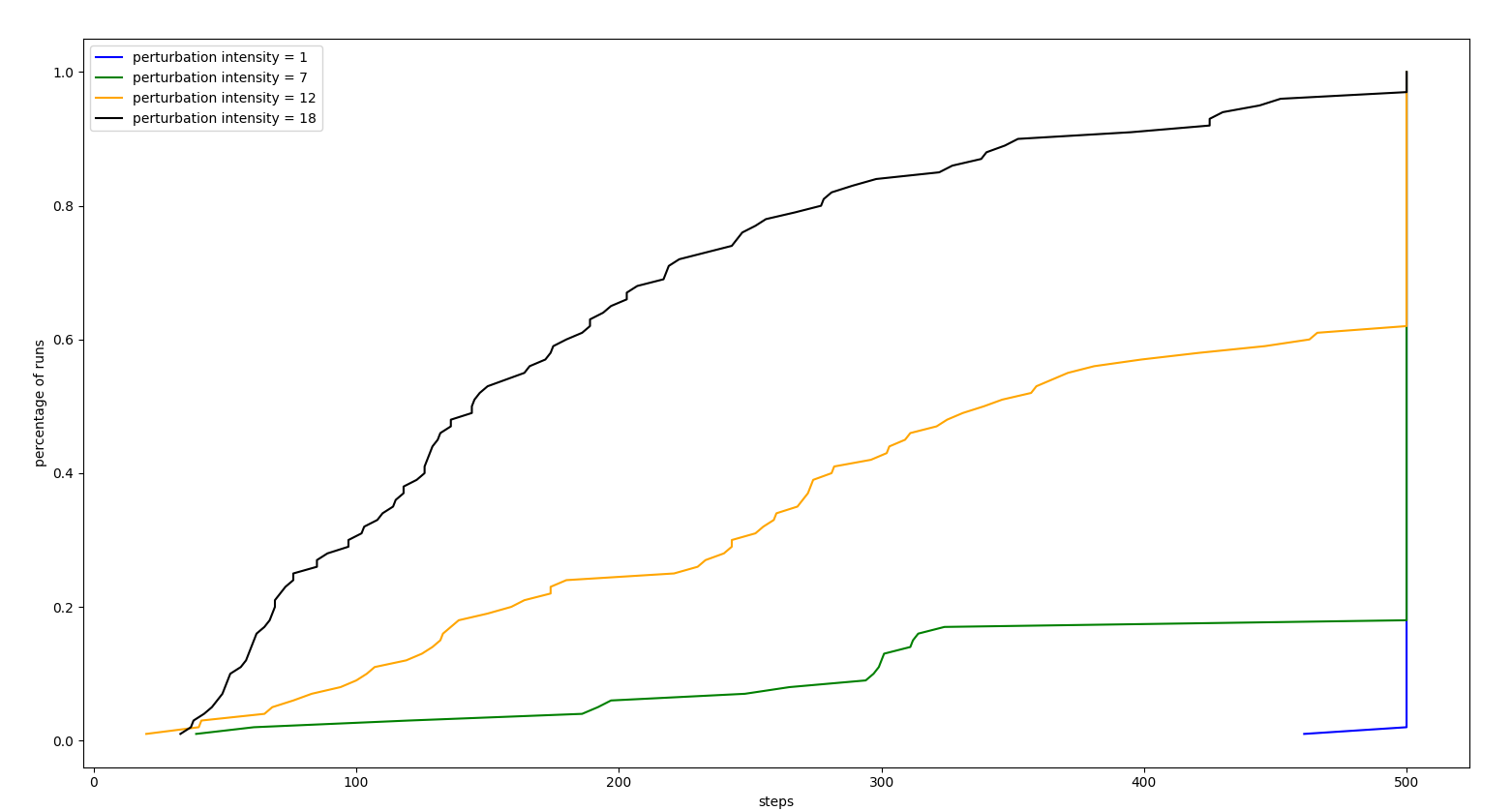
INTENSITY ANALYSIS

All the following experiments were performed with perturbation frequency 0.2 (perturbation in 20% of control iterations)

map

map

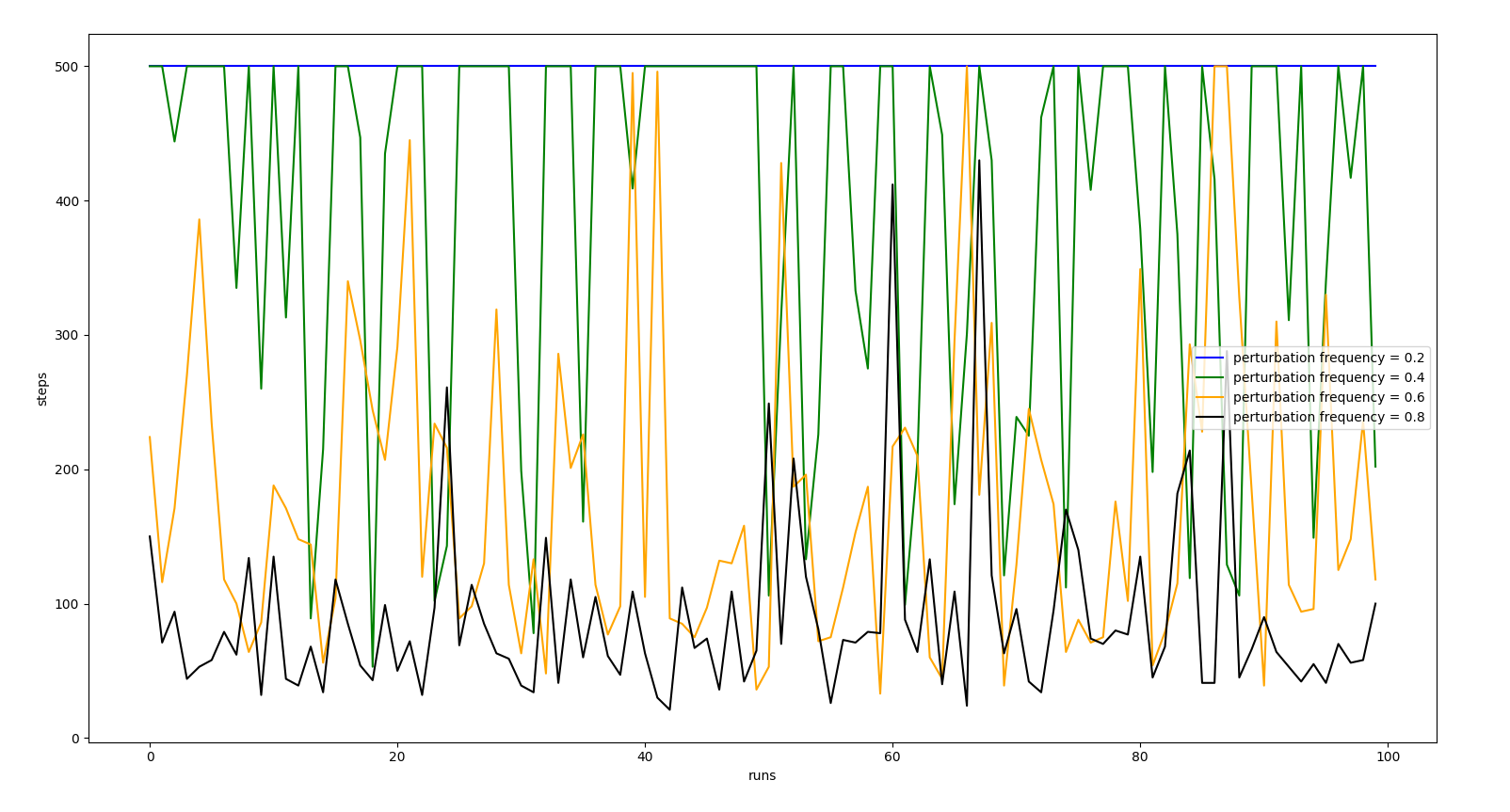
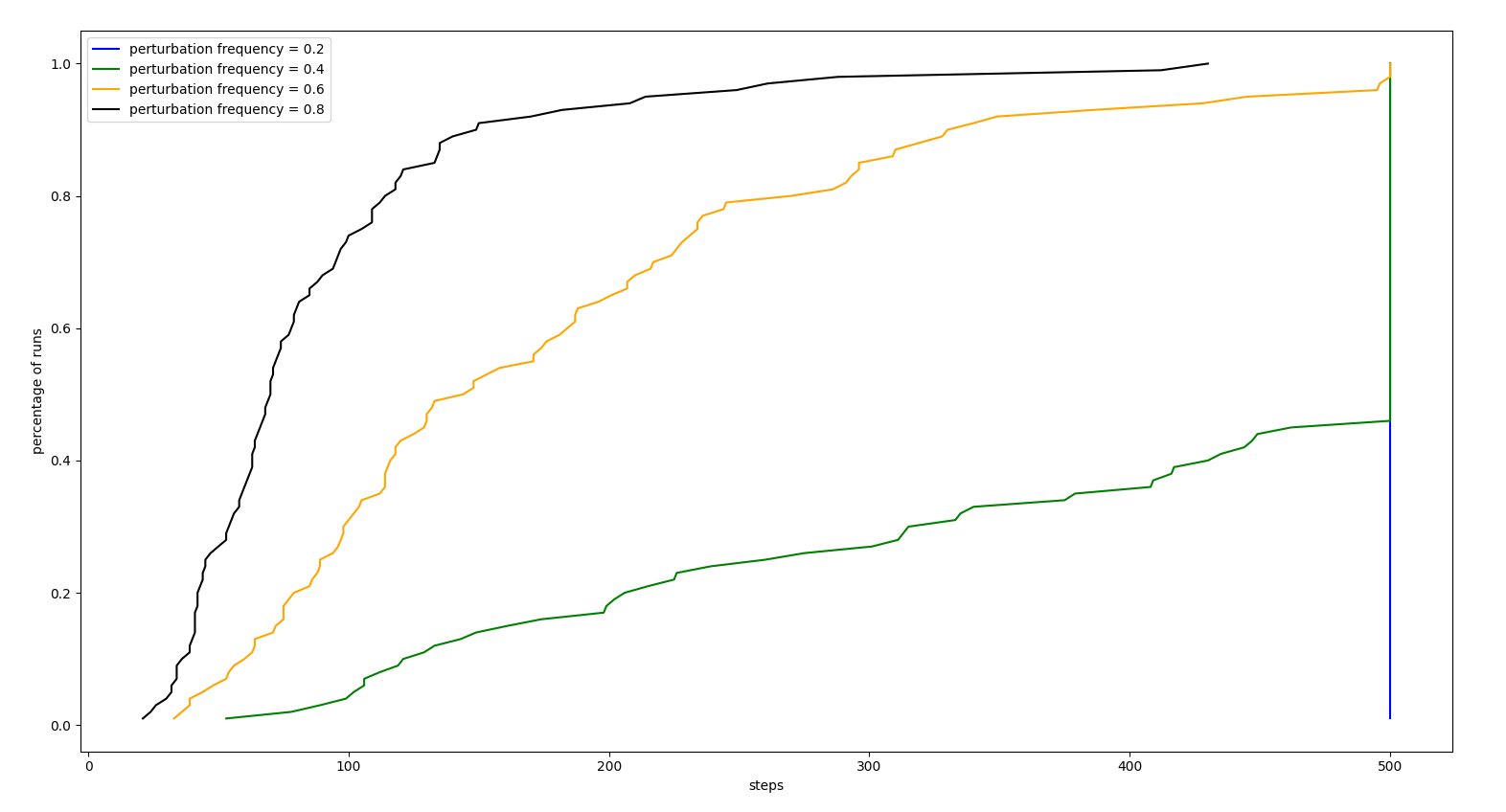
FREQUENCY ANALYSIS

All the following experiments were performed with perturbation intensity 1

map

map

Training with additive random perturbations

For the following experiments we will try to improve the results of the no perturbations trained agent in the following scenario configuration:

  • random_perturbations_level = 0.2 (perturbation in 20% of control iterations)
  • perturbation_intensity_std = 10

map

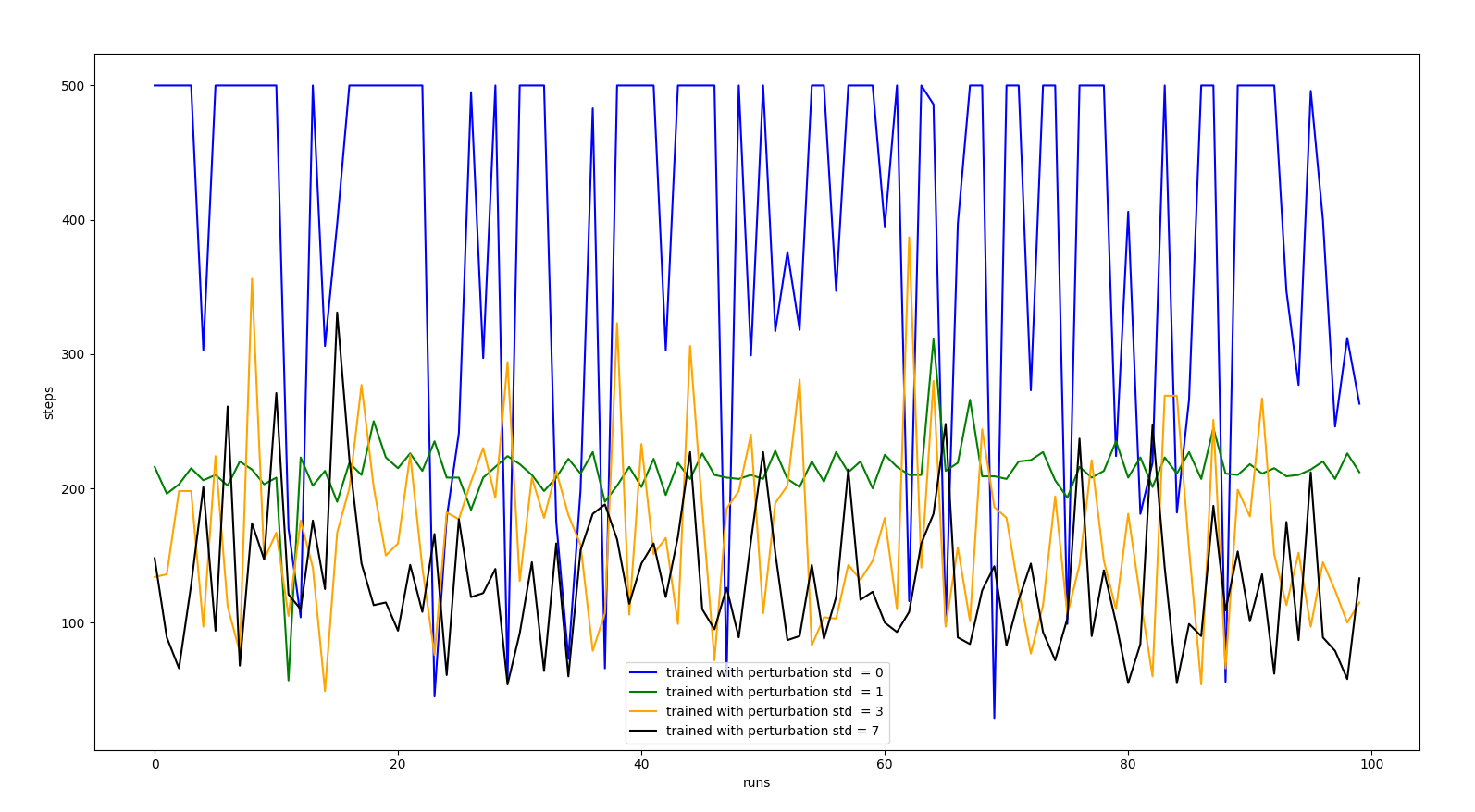
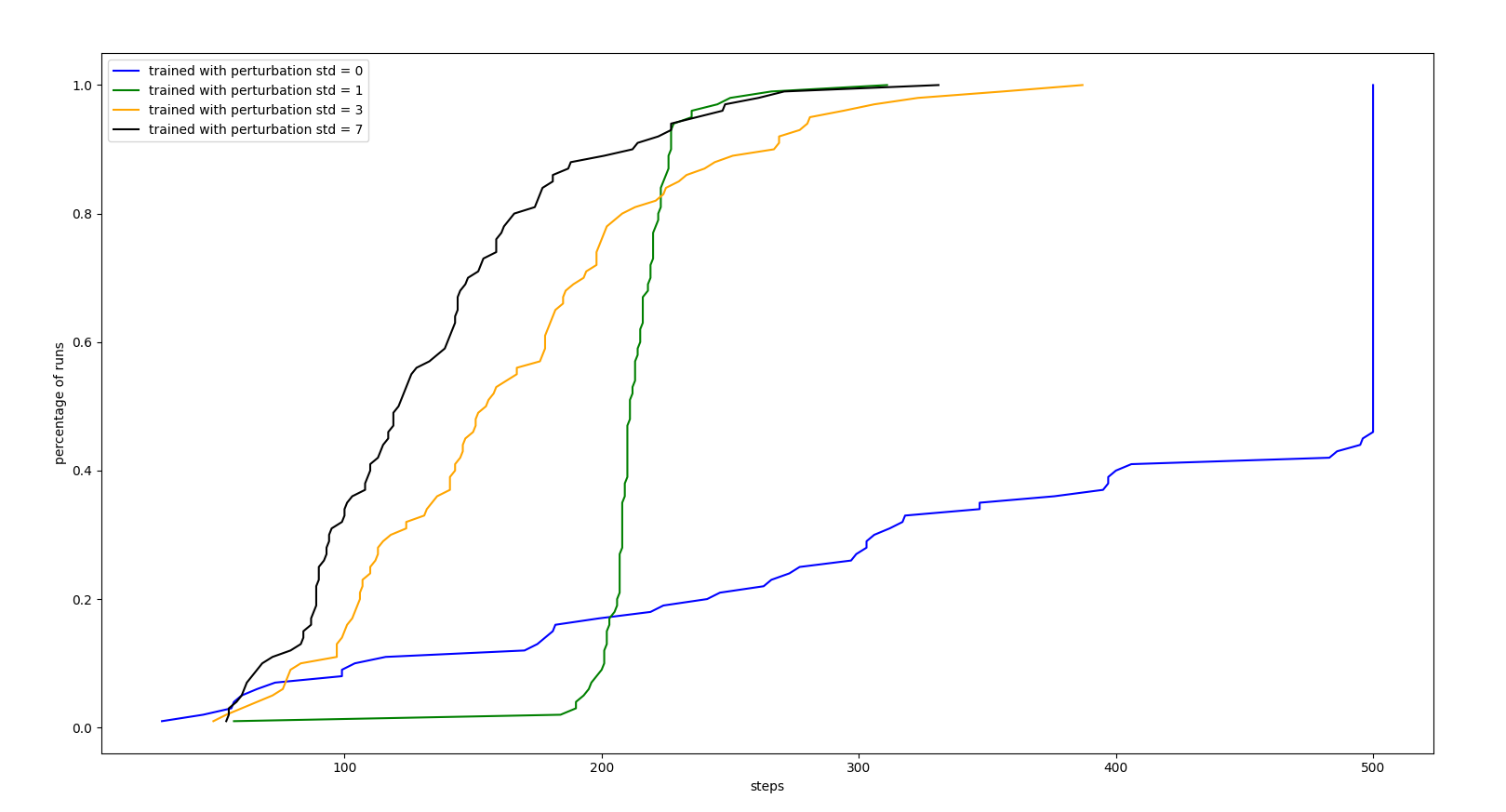
RANDOM PERTURBATIONS INTENSITY TRAINING EVALUATION

Now, instead of training the agent in ideal conditions, we will set the perturbation frequency to 0.1 and we will play with the intensity standard deviation of those perturbations.

map

map

RANDOM PERTURBATIONS FREQUENCY TRAINING EVALUATION

Now, instead of training the agent in ideal conditions, we will set the perturbation intensity to 1 and we will play with the frequency of those perturbations.

map

map

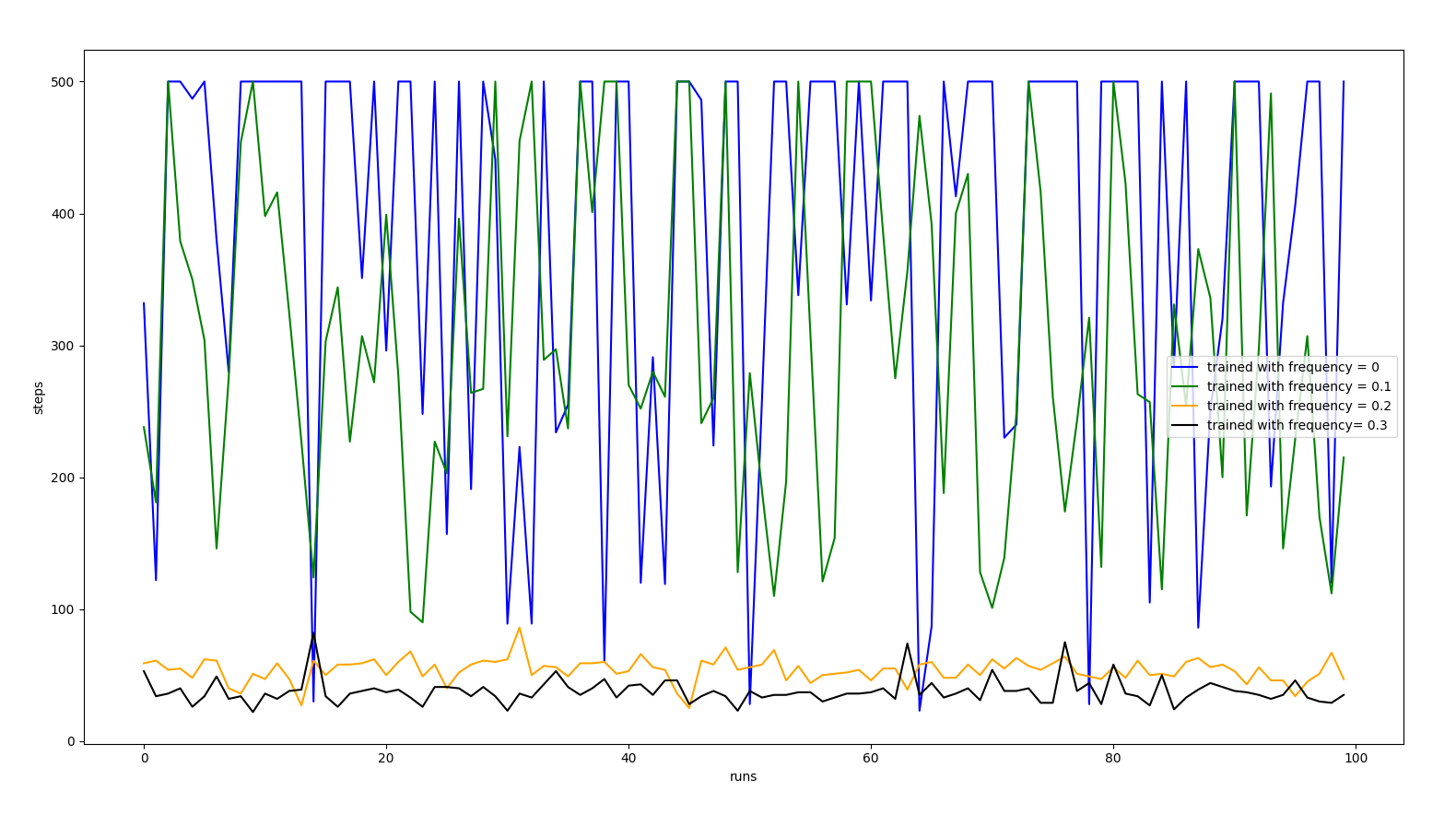
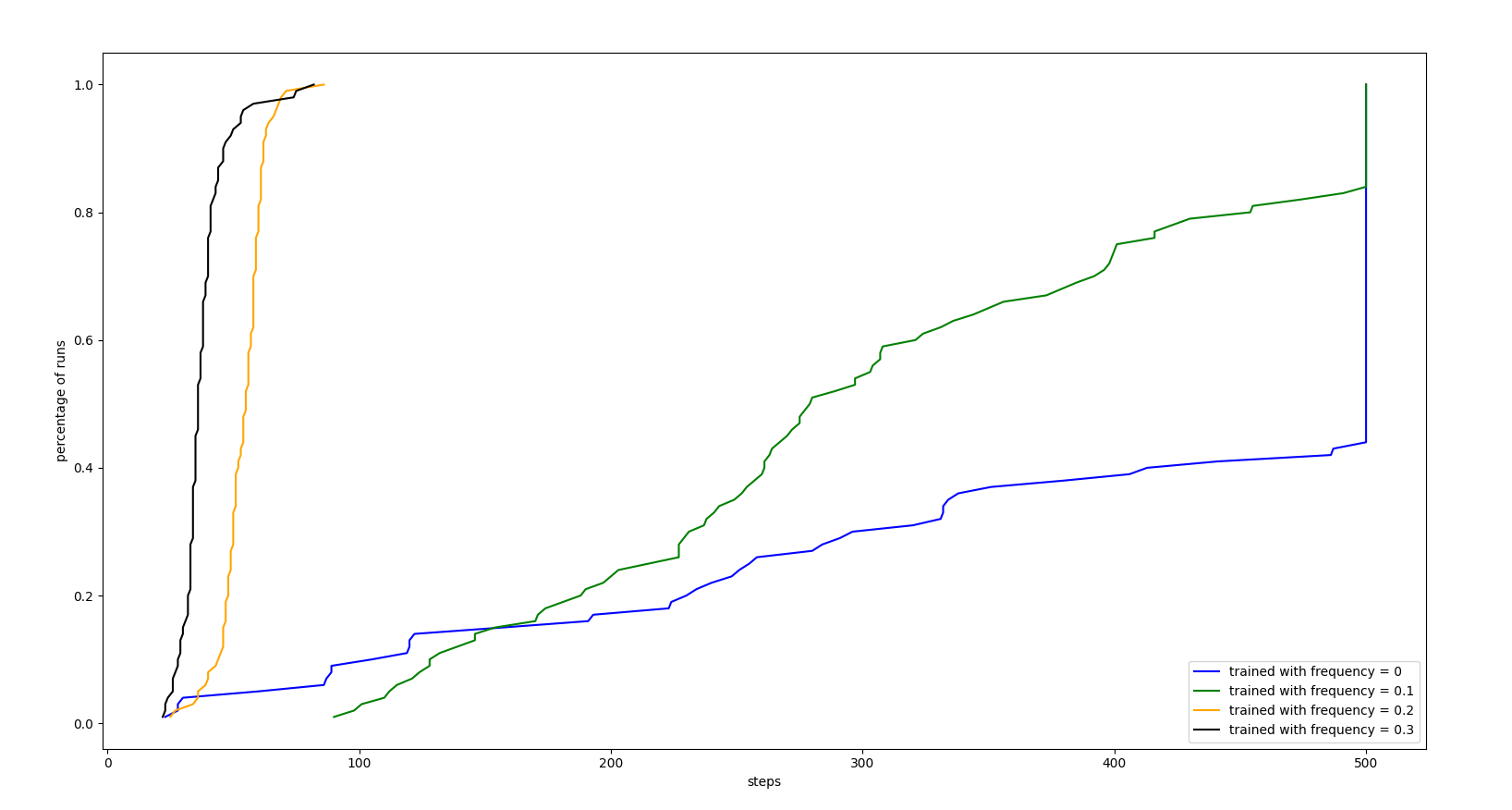
As we could see, none of them worked better than the agent trained with 0 perturbations noise. Our conclusion is that it didn’t help because the agent did not know if a perturbation was the problem or its action was not the right one so it made the situation worse.

INITIAL STATE

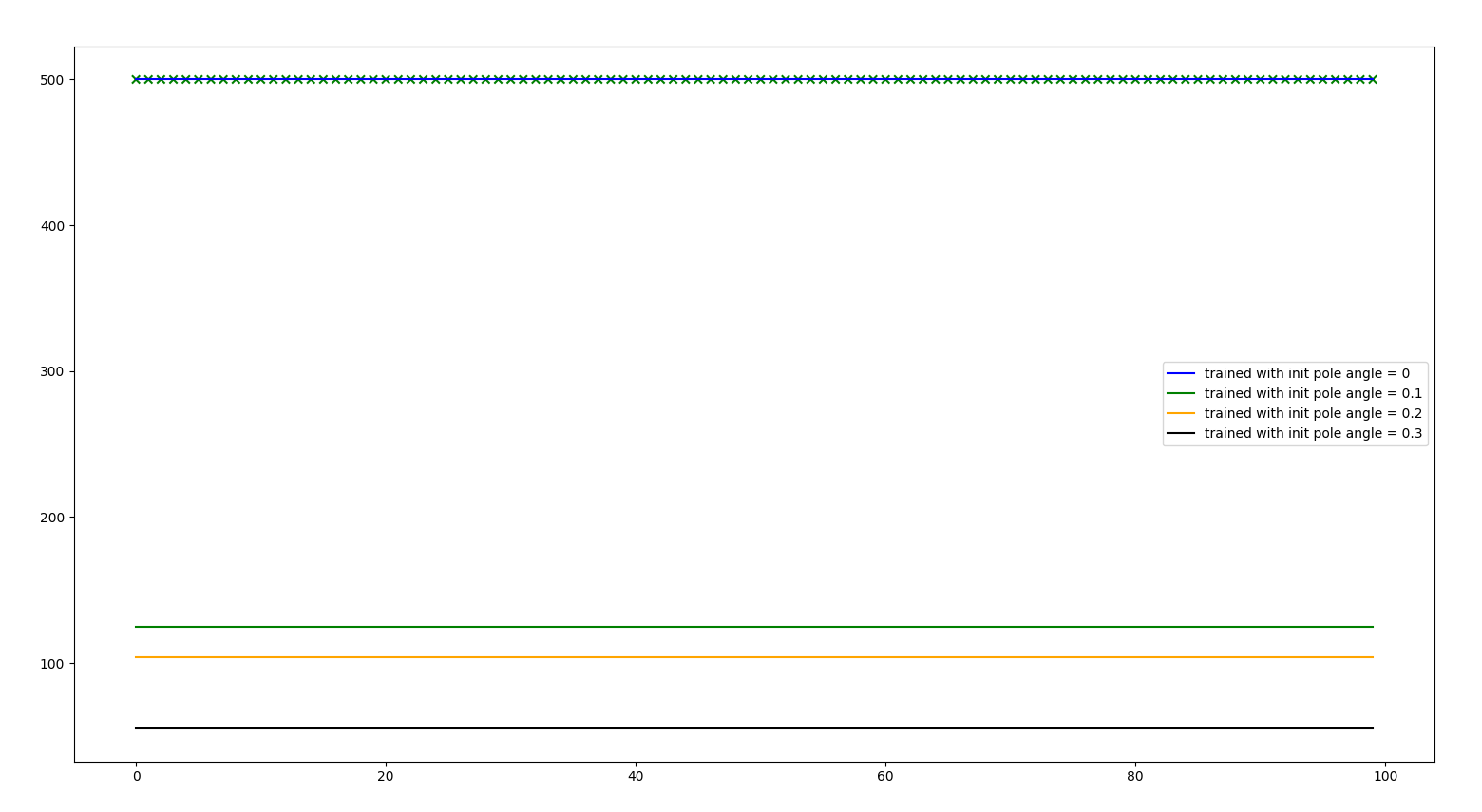
let’s see how solid is our agent in terms of initial position pole angle

Initial pole angle of 0.25

map

Initial pole angle of 0.3

map

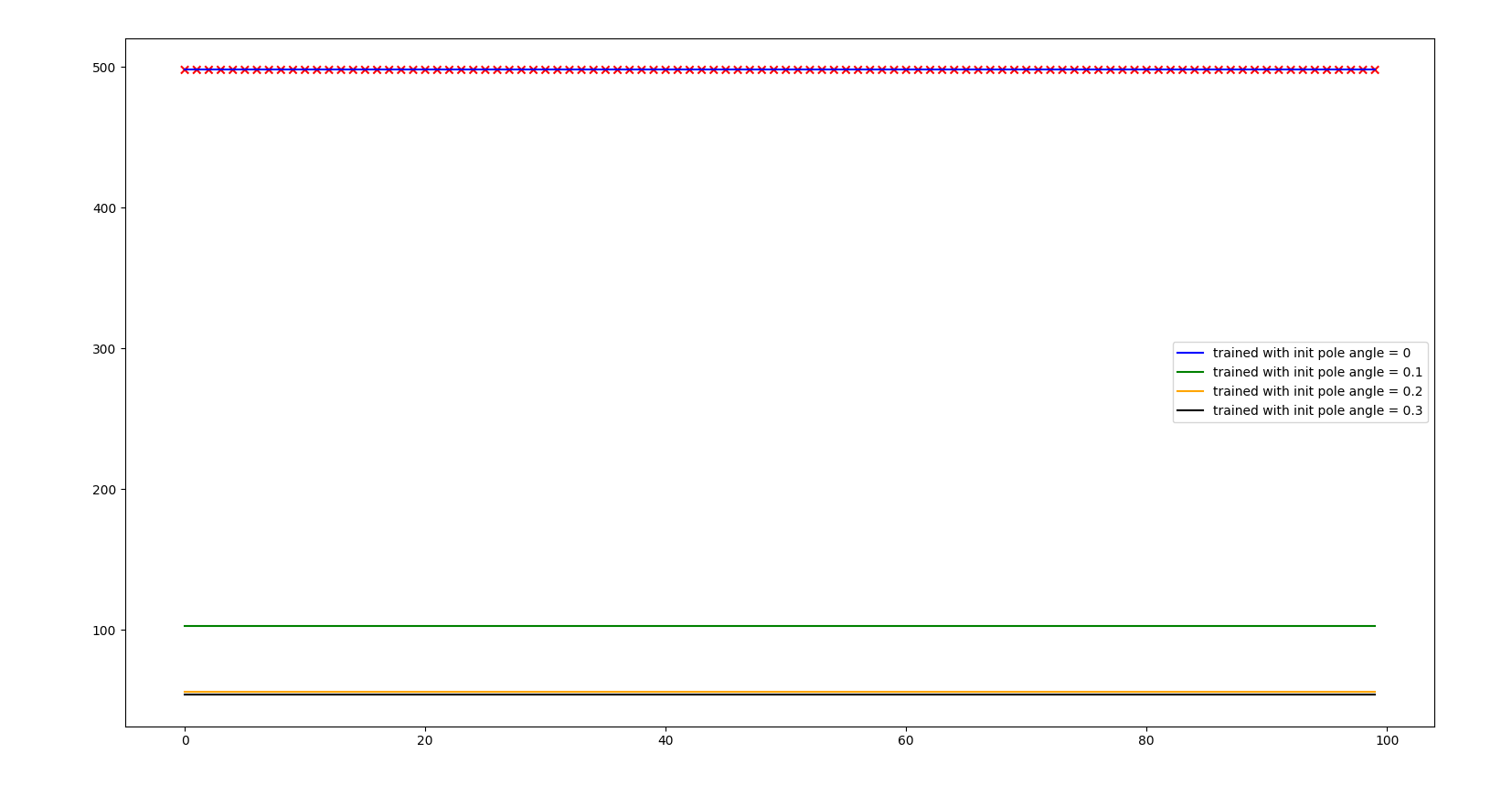
After the visualizations, we observed that the actions the agent was taken were correct (all the time push to the right to correct the pole angle), but it was not possible to recover the position within the constraints of the problem (iteration controls frequency and actions force) So it is not a problem of the agent not being able to recover, it is problem of the problem imposed, which given the environment conditions and the problem design, makes the solution impossible. It may work incresing the power of the actions and the granularity of them.

We also saw that adding initial pole angle to the training did not help to train a better agent

CONCLUSIONS

  • Training conditions needs to be feasible enough so the agent randomly learns the optimal actions to reach the objective
  • If you have a problem or an external agent that makes your scenario more complex, it is useless training in that scenario without giving a new input that model the problem external agent behavior.

TO EXPLORE

  • If the problem actions are too wide and the optimal actions impossible to learn in a randomly way, we can use iterative learning to make our agent learn how it has to behave (going gradually from the most basic scenario to the complex one)
  • Adaptative learning rate could help. (e.g torch implementation)

You May Also Enjoy