Semana 40. Preparación del ejercicio Amazon Warehouse y busqueda de una ruta óptima en la solución de referencia
Busqueda de una ruta óptima
En la solución de referencia para el ejercicio Amazon Warehouse se quiere encontrar la ruta más corta, para ello en la librería OMPL existe un tutorial donde explica cómo buscar la planificación óptima. En el tutorial indica que para definir un problema de planificación óptima hay que utilizar un planificador optimizado como por ejemplo el PRM, RRT o SPARS2 e indicar un objetivo de planificación que en nuestro caso sería encontrar la ruta de longitud más corta. En la siguiente página se lista todos los planificadores disponibles.
Modificando el ejemplo que ofrecen en el tutorial adaptandolo a nuestro problema la solución generada es la siguiente:
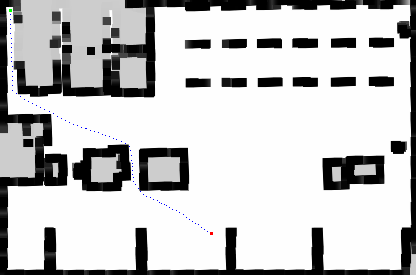
La ruta varía un poco en cada ejecución pero no difiere mucho con la imagen superior, en general la longitud oscila alrededor de 345.
Comprobación de la solución comparandolo con otras rutas
He intentado buscar diferentes caminos candidatos de ser la ruta más corta partiendo del código que utilicé la semana pasada basado en planificadores regulares he encontrado 3 rutas:
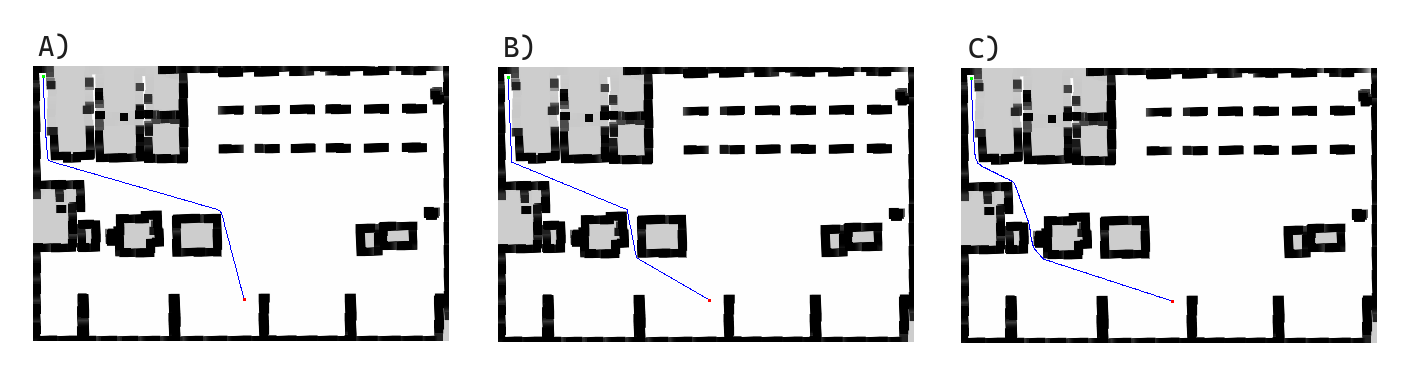
Y en la siguiente tabla muestro la longitud de cada una:
| Path | A | B | C |
|---|---|---|---|
| Path length | 356.1846464183808 | 342.87949967116003 | 348.4543349937395 |
Como se había mencionado anteriormente, hay baja probabilidad de generar dos rutas exactamente iguales, pero tras varias ejecuciones he llegado a la conclusión de que en casi todos los casos las soluciones aproximadas a la ruta B son las más cortas.
Investigando más …
Una de las opciones que ofrece la librería es establecer un tiempo límite de ejecución. Según lo explicado en el tutorial los planificadores regulares paran en la primera solución encontrada, sin embargo, los optimizados se paran cuando encuentran una ruta que cumple el objetivo de optimización. Sabiendo esto, he hecho pruebas alargando este tiempo y he observado que hay una mejora adicional a la ruta generada, la media de la longitud de los caminos ha mejorado a 340.
