Semana 18. Implementación de la densificación utilizando diferentes algoritmos de interpolación 1
Auto-interpolación
El primero de los algoritmos, se basa en interpolar los valores de un punto de la nube original. Al inicializar n_neighbor a 1, se toman los valores (x,y,z,r) del punto seleccionado aleatoriamente de la nube original y se crea un nuevo punto que tendrá un valor de r igual al punto seleccionado y las cordenadas x,y,z serán las coordenadas del punto seleccionado más un valor aleatorio entre -0.1 y 0.1.
El criterio para seleccinar los puntos que se interpolarán, es contar las veces que se toma un punto y elegir aleatoriamente entre los que menos se han seleccionado.
Este proceso se repite las veces necesaria para obtener un numero de puntos en la nube densificada igual al numero de puntos de la nube original multiplicado por el indice de densificación.
def densify_point_cloud(points: np.ndarray, remissions: np.ndarray,
density_factor: float = 5.0) -> Tuple[np.ndarray, np.ndarray, np.ndarray, np.ndarray]:
"""
Densifica la nube de puntos utilizando interpolación basada en vecinos más cercanos.
"""
# Usar NearestNeighbors para encontrar los vecinos más cercanos
nn = NearestNeighbors(n_neighbors=2)
nn.fit(points)
# Establecer el número de nuevos puntos a crear
num_new_points = int((len(points) * (density_factor-1)))
# Cuenta de las veces que se usa cada punto
point_usage_count = {}
# Almacenar los puntos y las intensidades generadas
new_points = []
new_remissions = []
for _ in range(num_new_points):
# Elegir un punto aleatorio de la nube de puntos original
index = np.random.randint(0, len(points))
point = points[index]
# Elegir un punto que haya sido usado menos veces
if not point_usage_count: # Si el diccionario está vacío
index = np.random.randint(0, len(points))
else:
# Encontrar el mínimo número de veces que se ha usado cualquier punto
min_usage = min(point_usage_count.values())
# Obtener todos los índices que tienen el mínimo uso
least_used_indices = [idx for idx, count in point_usage_count.items() if count == min_usage]
# Si hay puntos que aún no se han usado, incluirlos
unused_indices = [i for i in range(len(points)) if i not in point_usage_count]
candidate_indices = least_used_indices + unused_indices
# Seleccionar aleatoriamente entre los candidatos
index = np.random.choice(candidate_indices)
point = points[index]
# Incrementar contador para el punto seleccionado
if index in point_usage_count:
point_usage_count[index] += 1
else:
point_usage_count[index] = 1
# Obtener los 2 vecinos más cercanos (el primero es él mismo)
distances,indices = nn.kneighbors([point], n_neighbors=2)
# Seleccionar el segundo vecino más cercano para interpolar
neighbor_point = points[indices[0][1]]
print(f"\nPunto original seleccionado [{index}]: {point}")
print(f"Punto vecino encontrado [{indices[0][0]}]: {neighbor_point}")
print(f"¿Son el mismo punto?: {np.array_equal(point, neighbor_point)}")
# Interpolar entre el punto original y el vecino seleccionado
displacement = np.random.uniform(-0.1, 0.1, size=(3,)) # Pequeño desplazamiento aleatorio
interpolated_point = (point + neighbor_point) / 2 + displacement
# Las intensidades de los nuevos puntos serán las medias de las intensidades del punto original y el vecino
interpolated_remission = (remissions[index] + remissions[indices[0][1]]) / 2
# Agregar el nuevo punto y su intensidad
new_points.append(interpolated_point)
new_remissions.append(interpolated_remission)
# Mostrar el uso de los puntos
print("\nInformación de puntos usados como referencia:")
print("Formato: [Punto ID] (x, y, z) - usado N veces - Tipo")
for point_idx, count in point_usage_count.items():
coord = points[point_idx]
print(f"[{point_idx}] ({coord[0]:.3f}, {coord[1]:.3f}, {coord[2]:.3f}) - usado {count} veces - ORIGINAL")
# También podemos mostrar los nuevos puntos generados
print("\nPuntos nuevos generados:")
for i, new_point in enumerate(new_points):
print(f"[NEW_{i}] ({new_point[0]:.3f}, {new_point[1]:.3f}, {new_point[2]:.3f}) - INTERPOLADO")
# Convertir las listas a arrays
new_points = np.array(new_points)
new_remissions = np.array(new_remissions)
combined_points = np.vstack([points, new_points])
combined_remissions = np.concatenate([remissions, new_remissions])
# Retornar los puntos originales junto con los nuevos puntos
return combined_points, combined_remissions
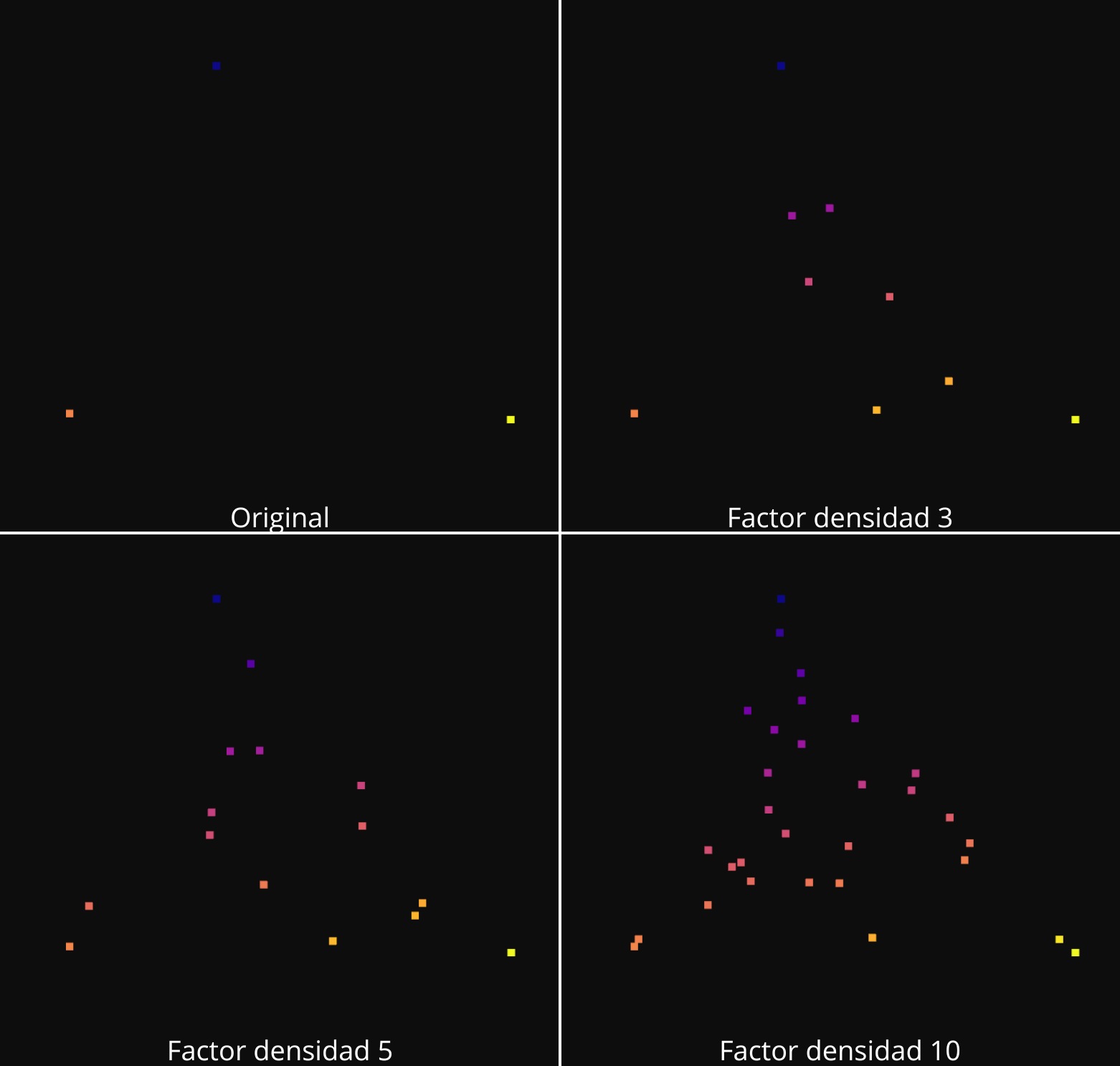
Visualización del aumento de la densidad con auto-interpolación:

1-NN
El siguiente algoritmo, 1-NN, sigue el mismo funcionamiento que el anterior. En este caso el valor de n_neighbor es 2. El primer paso es común con el algoritmo anterior. Se selecciona aleatoriamente un punto de la nube original. De este punto se selecciona el vecino más cercano. El nuevo punto tendrá unas coordenadas x,y,z, que se han generado calculando la media de las posiciones de los dos puntos, y se añade un desplazamiento aleatorio entre -0.1 y 0.1, para evitar coincidencias entre los puntos generados. Para el valor de r, también se calcula la media del valor de r del punto original seleccionado y su vecino mas cercano.
El proceso se repite tantas veces como sea necesario para lograr la densidad que se indique, es decir que el numero final de puntos sea igual al nuero original multiplicado por el factor de densificación.
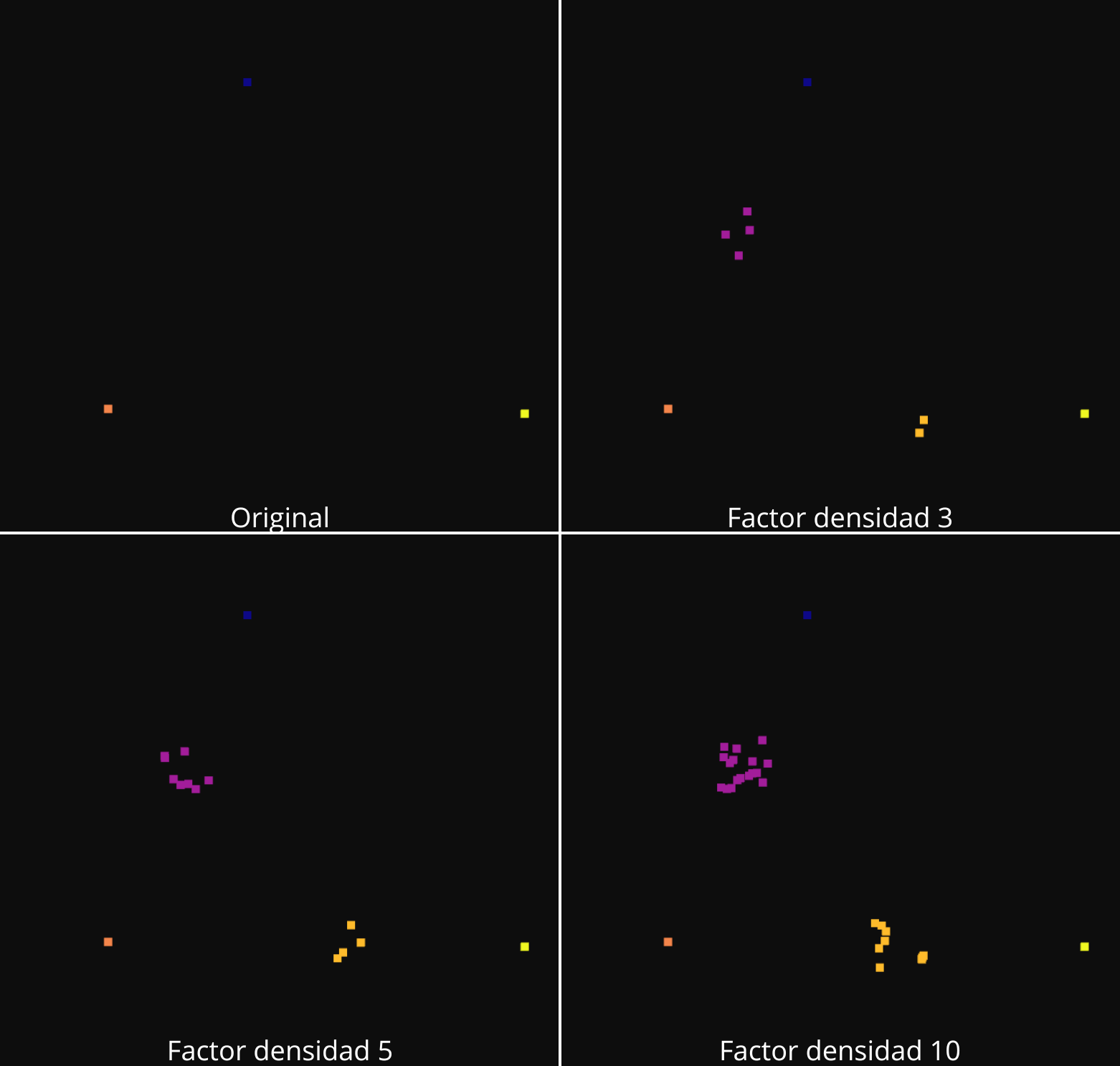
Aumento de la densidad con 1-NN:
TIN
En este caso se utiliza la triangulación de Delaunay para realizar la interpolación de los puntos. Este algoritmo consiste en crear un triańgulo usando las coordenadas x,y de los puntos de entrada, creando una malla triangular que conecta todos los puntos. Usando esta triangulación, el algoritmo LinearNDInterpolator creaa dos interpoladores lineales, uno para las coordenadas z y otro para los calores de intensidad.
# Crear la triangulación de Delaunay
tri = Delaunay(points[:, :2])
# Crear un interpolador lineal basado en la triangulación
z_interpolator = LinearNDInterpolator(tri, points[:,2])
remission_interpolator = LinearNDInterpolator(tri, remissions)
El proceso de densificación determina cuantos puntos nuevos se van a crear basandose en el factor de densificación density_factor. Genera coordenadas x,y aleatorias dentro de los limites de la nube de puntos original. Verifica si cada nuevo punto cae dentro de la triangualación, para los puntos validos, los que estan dentro de la trianguñación, interpola la coordenada z y los valores de intensidad usando los interpoladores lineales. Por ultimo se añaden los nuevos puntos a la nube depuntos, combinando los puntos originales y los nuevos.
# Establecer el número de nuevos puntos a crear
target_point = int(len(points) * density_factor)
# Generar nuevos puntos dentro del área de la triangulación
x_min, x_max = points[:, 0].min(), points[:, 0].max()
y_min, y_max = points[:, 1].min(), points[:, 1].max()
new_points = []
new_remissions = []
while len(new_points) + len(points) < target_point:
# Generar un punto aleatorio dentro del rango (x,y)
x = np.random.uniform(x_min, x_max)
y = np.random.uniform(y_min, y_max)
# Verificar si el punto está dentro de la triangulación
if tri.find_simplex(np.array([[x, y]])) >= 0:
# Interpolar el valor de z y la intensidad
z_interp = z_interpolator(x, y)
remission_interp = remission_interpolator(x, y)
if not np.isnan(z_interp):
new_points.append([x,y,z_interp])
new_remissions.append(remission_interp)
combined_points = np.vstack([points, new_points])
combined_remissions = np.concatenate([remissions, new_remissions])
# Retornar los puntos originales junto con los nuevos puntos
return combined_points, combined_remissions