Semana 19. Implementación de la densificación utilizando diferentes algoritmos de interpolación 2
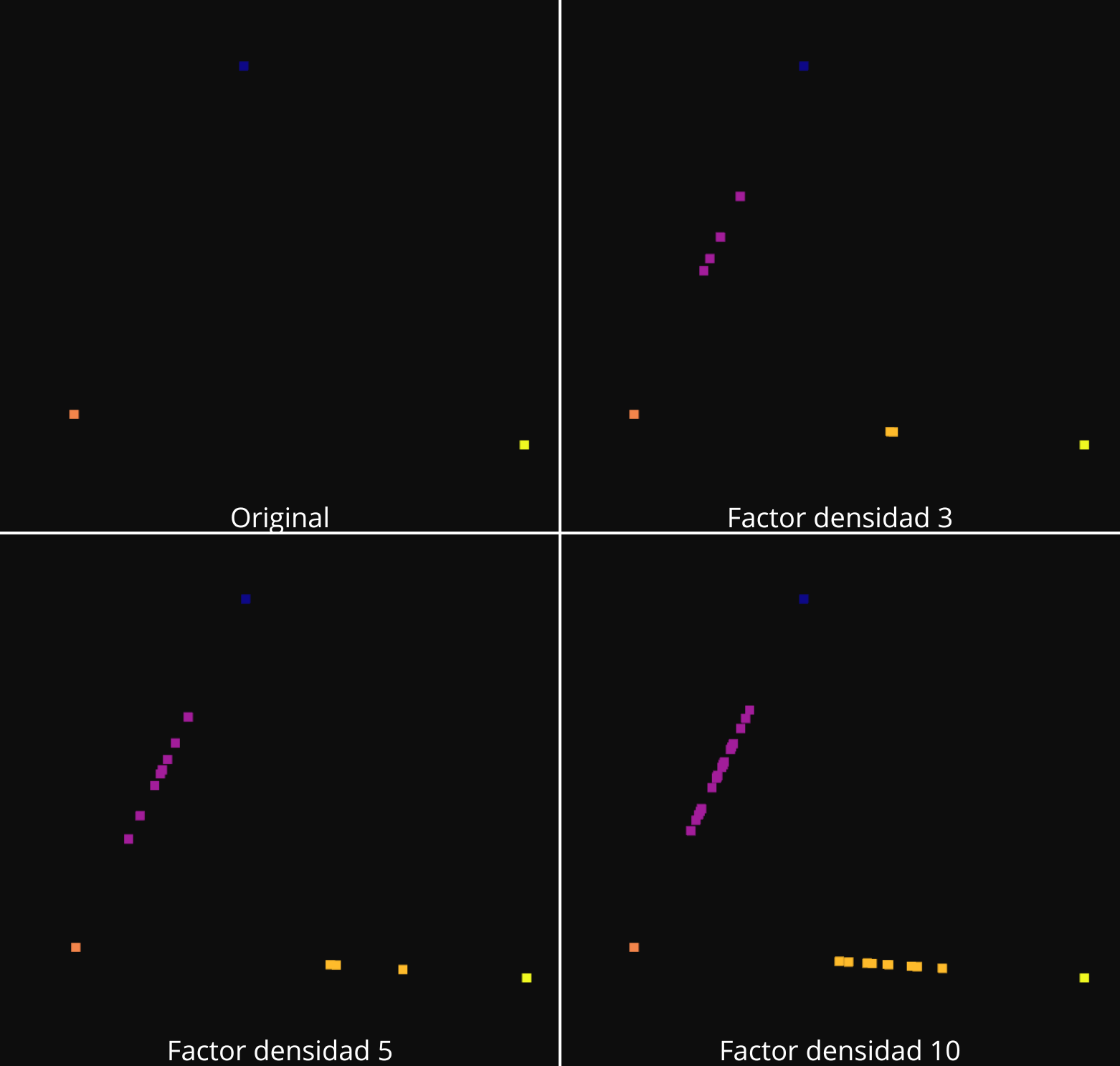
1-NN
He realizado modificaciones en el algoritmo 1-NN de manera que la posición del punto que se genera esté situado en el vector que une el punto seleccionado y su vecino mas cercano, siguiendo la fórmula C = A + α(B-A). Siendo C el punto generado, A el punto original seleccionado , Bsu vecino mas cercano y λ un factor aleatorio que sige una distribución gaussiana.
# Interpolar entre el punto original y el vecino aplicando C = A + α(B - A)
displacement = np.random.normal(loc=0.5, scale=0.1) # Media 0.5 desviación 0.1
interpolated_point = point + displacement * (neighbor_point - point)
Aumento de la densidad con 1-NN:
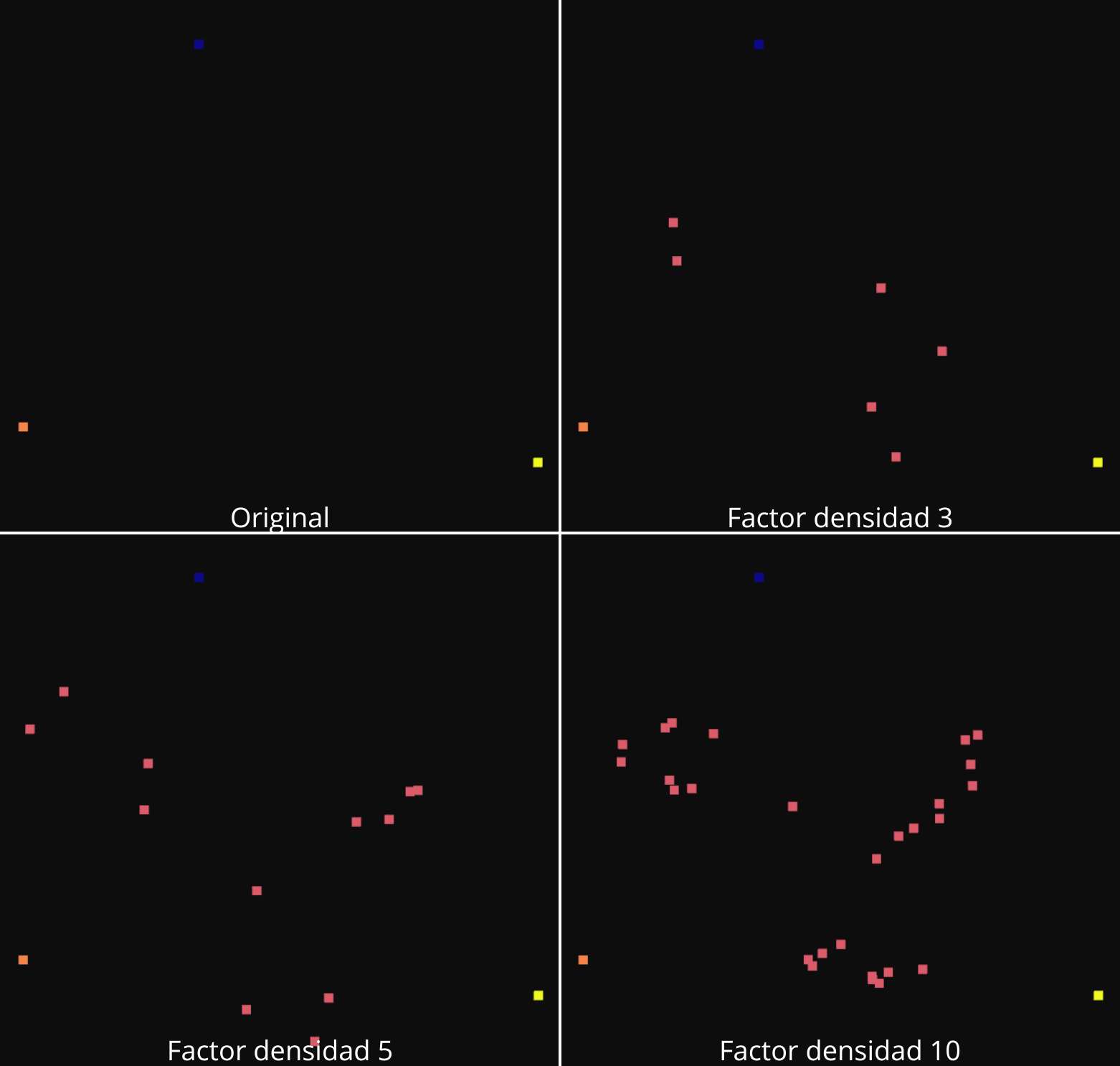
2-NN
De la misma manera que el caso anterior he implementado una densificación utilizando 2-NN, en este caso se tendran en cuenta los valores de los dos vecinos más cercanos. Las coordenadas del punto generado siguen la fórmula D = A + α(B-C) + β(C-A). Donde D el punto generado, A el punto original seleccionado , By C sus vecinos mas cercanos y α y β dos factores aleatorios que siguen una distribución gaussiana.
# Interpolar entre el punto original y los 2 vecino seleccionado aplicando D = A + α(B - A) + β(C - A)
alpha = np.random.normal(loc=0.5, scale=0.1) # Media 0.5 desviación 0.1
beta = np.random.normal(loc=0.5, scale=0.1) # Media 0.5 desviación 0.1
interpolated_point = point + alpha * (neighbor1 - point) + beta * (neighbor2 - point)
Aumento de la densidad con 2-NN:
IDW
Para solucionar el problema con la interpolacion de los valores de r, implemento el algoritmo de Interpolación Ponderada por Distancia Inversa o IDW (del inglés Inverse Distance Weighted). De esta manera se dá más peso a los puntos más cercaos y se reduce el peso de los más alejados, lo que permite una interpolación más precisa y suave.
Interpolación de la posición de los puntos
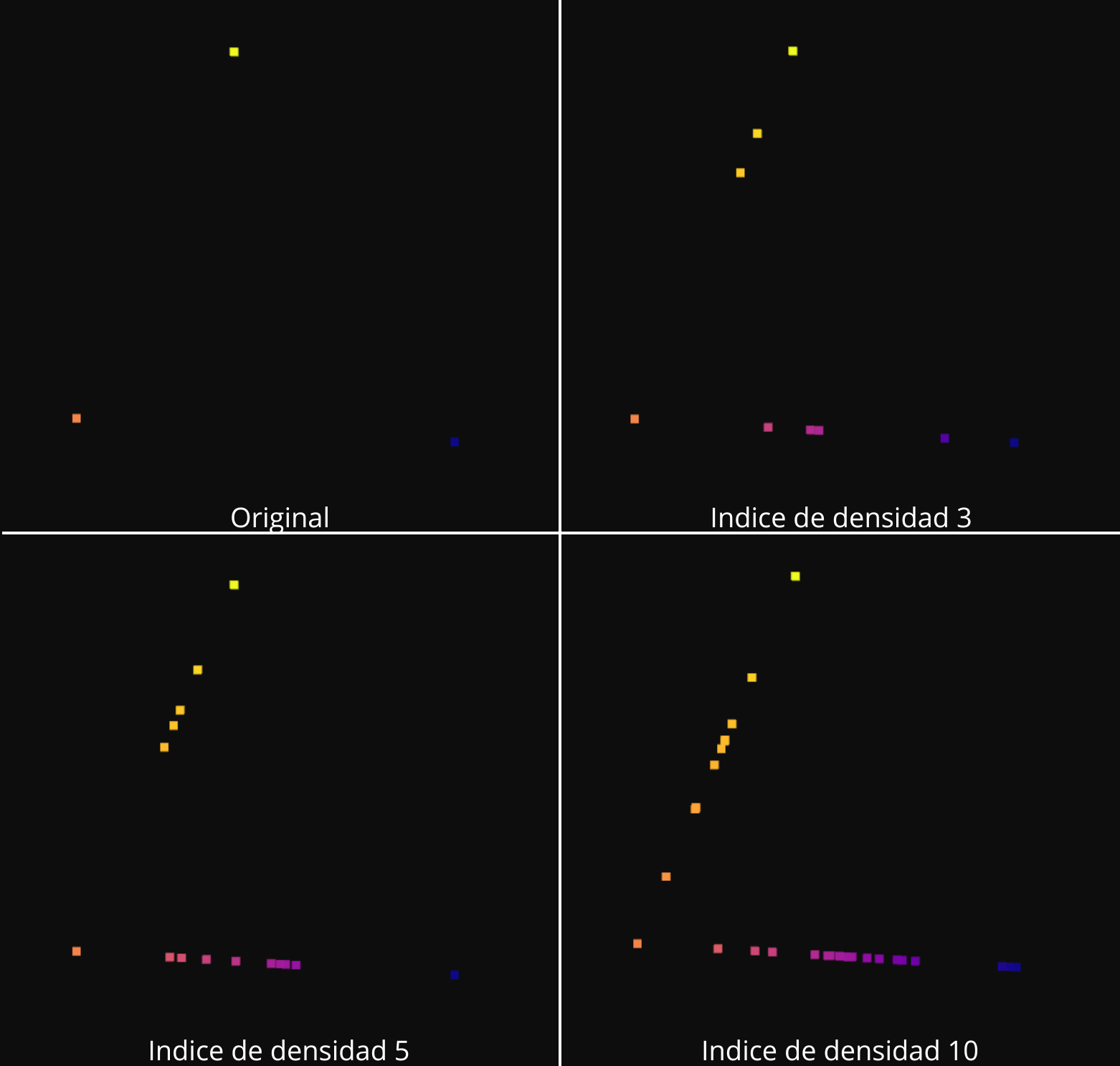
Utilizando 2 puntos
Cuando se utilizan 2 puntos para la interpolación, la posición de los nuevos puntos se calculan utilizando un cobinacion convex del punto original (A) y su vecino más cercano (B). La formula utilizada es :
C = λ·A + (1-λ)·B
Donde λ es un peso aleatorio que sigue una distribución normal truncada en el rango [0, 1]. λ se genera utilizando spicy.stats.truncnorm , lo que gartantiza que los valores cercanos a 0.5 sean más probables y los valores cercanos a 0 y 1 sean menos probables.
from scipy.stats import truncnorm
# Parámetros de la distribución normal truncada
media = 0.5
desviacion_estandar = 0.2
limite_inferior = 0
limite_superior = 1
# Convertir los límites al espacio de la distribución normal estándar
a = (limite_inferior - media) / desviacion_estandar
b = (limite_superior - media) / desviacion_estandar
# Generar lambda con distribución normal truncada
lambdaComb = truncnorm.rvs(a, b, loc=media, scale=desviacion_estandar)
lambdaComb = np.clip(lambdaComb, 0.0, 1.0) # Asegurarse de que esté en el rango [0, 1]
# Interpolación aplicando C = λA + (1-λ)B
interpolated_point = lambdaComb * point + (1 - lambdaComb) * neighbor_point
Utilizando 3 puntos
Cuando se utilizan 3 puntos, la posición de los nuevos puntos se calcula utilizando una combinación convexa de tres puntos: el punto original (A) y sus dos vecinos más cercanos (B y C). La formula utilizada es :
D = λ1·A + λ2·B + λ3·C
Donde λ1, λ2 y λ3 son pesos aleatorios que siguen una distribución normal truncada en el rango [0, 1]. Los pesos se normalizan para que sumen 1, lo que garantiza que la combinación sea convexa.
# Generar pesos aleatorios que sumen 1
lambda_1 = truncnorm.rvs(a ,b, loc=media, scale=desviacion_estandar)
lambda_2 = truncnorm.rvs(a ,b, loc=media, scale=desviacion_estandar)
lambda_3 = truncnorm.rvs(a ,b, loc=media, scale=desviacion_estandar)
# Normalizar los pesos para que sumen 1
total = lambda_1 + lambda_2 + lambda_3
lambda_1 /= total
lambda_2 /= total
lambda_3 /= total
# Interpolacion aplicando D=λ1*A+λ2*B+λ3*C
interpolated_point = lambda_1 * point_A + lambda_2 * point_B + lambda_3 * point_C
Interpolación del valor de r Para calcular el valor interpolado de r (remission), se utiliza la fórmula de IDW, que pondera los valores de r de los puntos originales en función de sus distancias al punto generado. La formula es:
r'=\frac{\frac{1}{d_{A}}*r_{A}+\frac{1}{d_{B}}*r_{B}+\frac{1}{d_{C}}*r_{C}}{\frac{1}{d_{A}}+\frac{1}{d_{B}}+\frac{1}{d_{C}}}
Donde r' es el valor de r interpolado de r. dA, dB y dC son las distancias entre el punto generado y los puntos originales que se han tomado de la nube. rA, rB y rC son los valores de r de los puntos originales.
# Calcular las distancias d_A, d_B y d_C
d_A = np.linalg.norm(interpolated_point - point_A) # Distancia al punto original
d_B = np.linalg.norm(interpolated_point - point_B) # Distancia al primer vecino
d_C = np.linalg.norm(interpolated_point - point_C) # Distancia al segundo vecino
# Aplicar la fórmula de interpolación para la remisión
r_A = remissions[index] # Remisión del punto original
r_B = remissions[indices[0][1]] # Remisión del primer vecino
r_C = remissions[indices[0][2]] # Remisión del segundo vecino
# Fórmula de interpolación de la remisión
interpolated_remission = ( (1/d_A) * r_A + (1/d_B) * r_B + (1/d_C) * r_C ) / ( (1/d_A) + (1/d_B) + (1/d_C) )
Visualización de resultados
Interpolación con 2 puntos
Cuando se utilizan 2 puntos para la interpolación, los nuevos puntos se generan a lo largo del vector que une el punto original con su vecino más cercano.

Interpolación con 3 puntos
Al utilizar 3 puntos, los nuevos puntos se generan dentro del plano formado por los tres puntos originales. Esto permite una mayor flexibilidad en la distribución de los puntos generados.
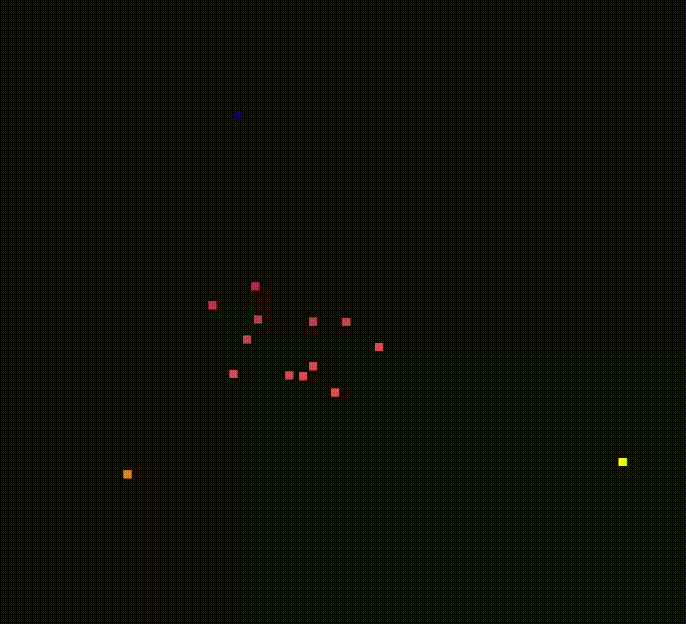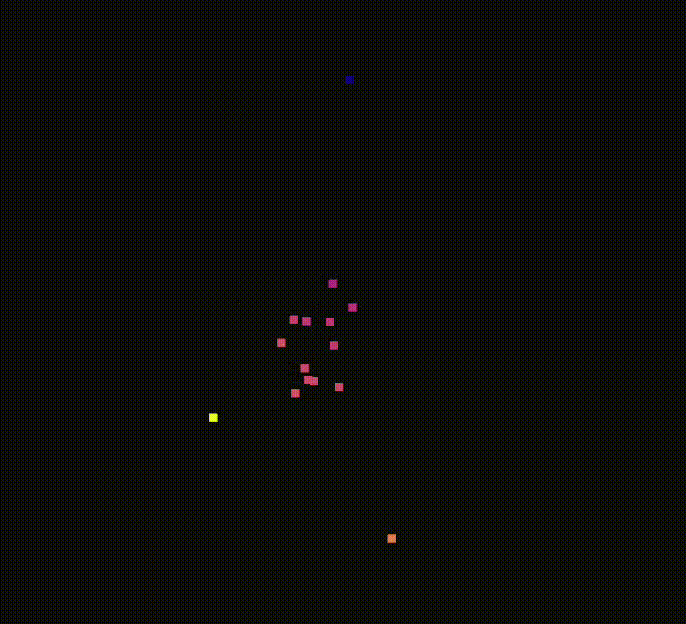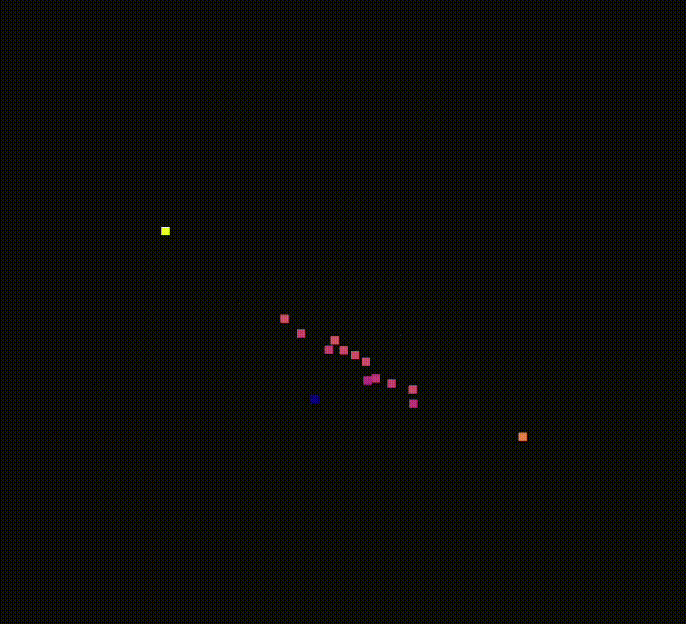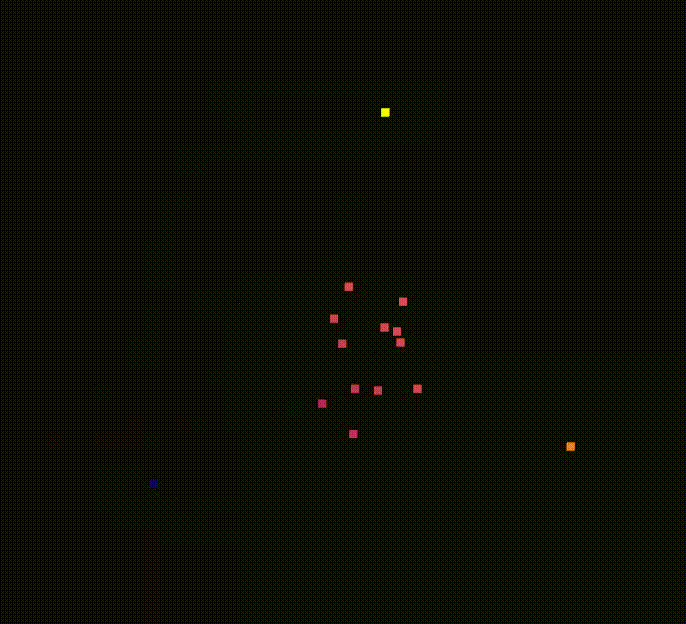
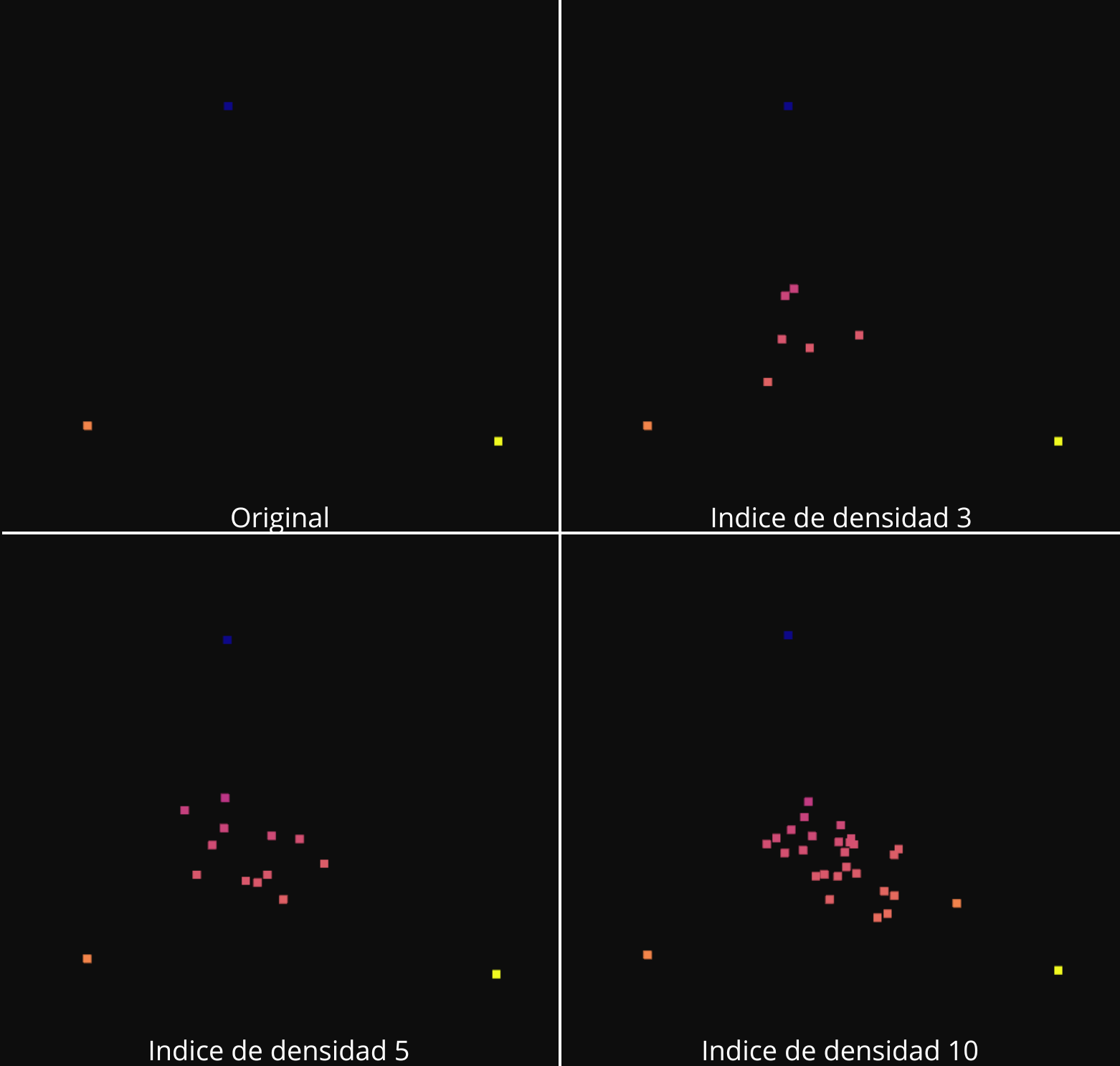
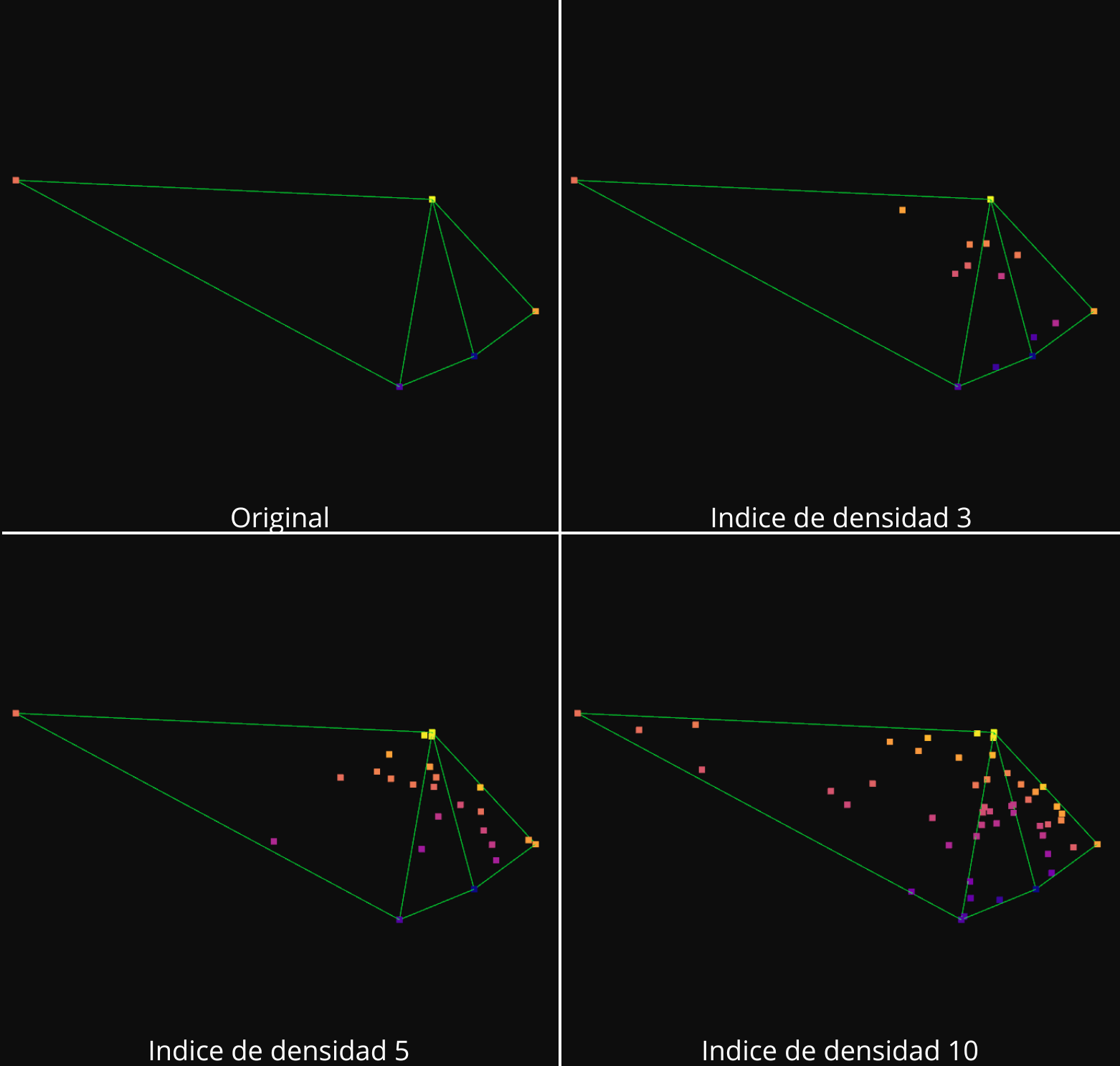
TIN
He mejorado el algoritmo de interpolacion triangular, de manera que los puntos nuevos se generen en el plano que forma cada triangulo de Dalunay. Para ello se realiza la triangulacion de Delaunay utilizando unicamente las coordenadas x e y. Esto genera una malla de triángulos en dos dimensiones, que se extiende sobre el plano horizontal. Después se calcula el número de puntos nuevos que hay que generar en funcion del indice de densisdad

# Crear la triangulación de Delaunay
tri = Delaunay(points[:, :2]) # Toma las coordenadas (x, y) para la triangulación
# Calcular el número de nuevos puntos a crear
num_original_points = len(points)
num_new_points = int(num_original_points * (density_factor-1))
# Calcular el número de puntos a generar por triángulo
num_triangles = len(tri.simplices)
points_per_triangle = num_new_points // num_triangles
remaining_points = num_new_points % num_triangles
A continuación se itera sobre cada triángulo generado por la triangulación de Delaunay. Para cada triángulo, se seleccionan las coordenadas y los valores de intensidad de los 3 vértices que lo forman. Y se calcula cuántos puntos nuevos se deben generar en ese triángulo.
for i, simplex in enumerate(tri.simplices):
# Obtener los vértices del triángulo
triangle_vertices = points[simplex] # Selecciona las coordenadas de los vertices que forma el triangulo
triangle_remissions = remissions[simplex] # intensidades de los vertices del triángulo
# Calcular el número de puntos para este triángulo
# points_per_triangle es el número base de puntos a generar por triángulo
# remaining_points es el resto de puntos que no se han distribuido uniformemente
# Si el índice del triángulo (i) es menor que remaining_points, se genera un punto adiciona
num_points_this_triangle = points_per_triangle + (1 if i < remaining_points else 0)
Para cada triángulo se generan puntos dentro de él. Se generan coordenadas baricéntricas aleatorias (w1, w2, w3) que definen la posicion del nuevo punto dentro del triángulo. Estas coordenadas se calculan utilizando las fórmulas de coordenadas baricéntricas:
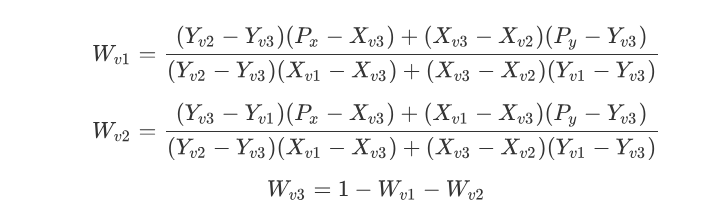
# Generar nuevos puntos dentro del triangulo actual
for _ in range(num_points_this_triangle):
# Vértices del triángulo (V1, V2, V3)
V1, V2, V3 = triangle_vertices
Px, Py = new_point[0], new_point[1] # Coordenadas x e y del nuevo punto
# Denominador común para w1 y w2
denominator = (V2[1] - V3[1]) * (V1[0] - V3[0]) + (V3[0] - V2[0]) * (V1[1] - V3[1])
# Calcular w1 y w2 usando las fórmulas de coordenadas baricéntricas
w1 = ((V2[1] - V3[1]) * (Px - V3[0]) + (V3[0] - V2[0]) * (Py - V3[1])) / denominator
w2 = ((V3[1] - V1[1]) * (Px - V3[0]) + (V1[0] - V3[0]) * (Py - V3[1])) / denominator
w3 = 1 - w1 - w2
Se calcula las coordenadas del nuevo punto como una combinación lineal de los vertices del triangulo, ponderados por las coordenadas baricéntricas (w1, w2, w3)
# Calcular el punto en el plano del triángulo
new_point = w1* triangle_vertices[0] + w2* triangle_vertices[1] + w3 * triangle_vertices[2]
El valor de la intensidad del nuevo punto se calcula como una combinación lineal de los valores de intensidad de los vertices, ponderados por las coordenadas baricéntricas. Finalmente se almacena el nuevo punto y su intensidad en las listas de puntos y remisiones.
# Calcular la intensidad usando interpolación ponderada por distancia inversa
# Las coordenadas baricéntricas (r1, r2, w3) ya son ponderaciones normalizadas
remission_interp = w1* triangle_remissions[0] + w2* triangle_remissions[1] + w3 * triangle_remissions[2]
# Agregar el nuevo punto y su intensidad a la lista
new_points.append(new_point)
new_remissions.append(remission_interp)
Aumento de la densidad con Interpolación Triangular: