Semana 23. Optimización de los metodos de densificación:Vectorización de TIN e IDW

Esta semana he realizado una optimización de los algoritmos de densificación TIN (Triangulated Irregular Network) e IDW (Inverse Distance Weighting), eliminando los bucles y sustituyendolos por operaciones matriciales vectorizadas. Este cambio ha significado una mejor significativa en el rendimiento computacional.

En ambos casos (TIN e IDW) los puntos se cargan como arrays NumPy 2D con forma (N, 3) y (N, 1) donde N es el número de puntos y 3 corresponde las coordenadas (x,y,z).

Optimización en el metodo TIN

Los principales cambios realizados en el algoritmo TIN incluyen:

• Generación vectorizada de coordenadas baricéntricas: Donde antes se usaban bucles for para generar los puntos en cada triángulo, ahora se generan matrices de todas las coordenadas baricéntricas en una sola operación.

• Interpolación vectorizada de puntos y valores: Se utilizan operaciones matriciales para calcular todos los nuevos puntos en una sola ejecución.

La nueva función encargada de la aplicacionde este método es la siguiente:

def densify_point_cloud(points: np.ndarray, remissions: np.ndarray, 
                        density_factor: float = 5.0) -> Tuple[np.ndarray, np.ndarray]:
    """
    Densifica la nube de puntos utilizando triangulación de Delaunay e interpolación lineal.
    """

    # Crear la triangulación de Delaunay
    tri = Delaunay(points[:, :2])  # Toma las coordenadas (x, y) para la triangulación

    # Calcular el número de nuevos puntos a crear
    num_original_points = len(points)
    num_new_points = int(num_original_points * (density_factor-1))

    # Calcular el número de puntos a generar por triángulo
    num_triangles = len(tri.simplices)

    # Distribuir puntos por los trangulos
    base_points_per_tri = num_new_points // num_triangles
    extra_points = num_new_points % num_triangles

    # Crear máscara para triángulos que reciben punto extra
    extra_mask = np.zeros(num_triangles, dtype=bool)
    extra_mask[:extra_points] = True
        
    # Vector de conteo de puntos por triángulo
    points_per_triangle = np.full(num_triangles, base_points_per_tri)
    points_per_triangle[extra_mask] += 1

    # Generar coordenadas baricéntricas para todos los puntos
    total_points = np.sum(points_per_triangle)

    # Generar coordenadas aleatorias
    w1_w2 = np.random.rand(total_points, 2)
    mask = w1_w2.sum(axis=1) > 1
    w1_w2[mask] = 1 - w1_w2[mask]
    w3 = 1 - w1_w2.sum(axis=1)
    barycentric = np.column_stack((w1_w2, w3))

    # Asignar triángulos a cada punto nuevo
    triangle_indices = np.repeat(np.arange(num_triangles), points_per_triangle)

    # Obtener vértices para cada punto nuevo
    vertices = points[tri.simplices[triangle_indices]]
    vertex_remissions = remissions[tri.simplices[triangle_indices]]

    # Interpolación vectorizada
    new_points = np.sum(barycentric[:, :, None] * vertices, axis=1)
    new_remissions = np.sum(barycentric * vertex_remissions, axis=1)

    # Combinar resultados
    combined_points = np.vstack([points, new_points])
    combined_remissions = np.concatenate([remissions, new_remissions])
    
    return combined_points, combined_remissions

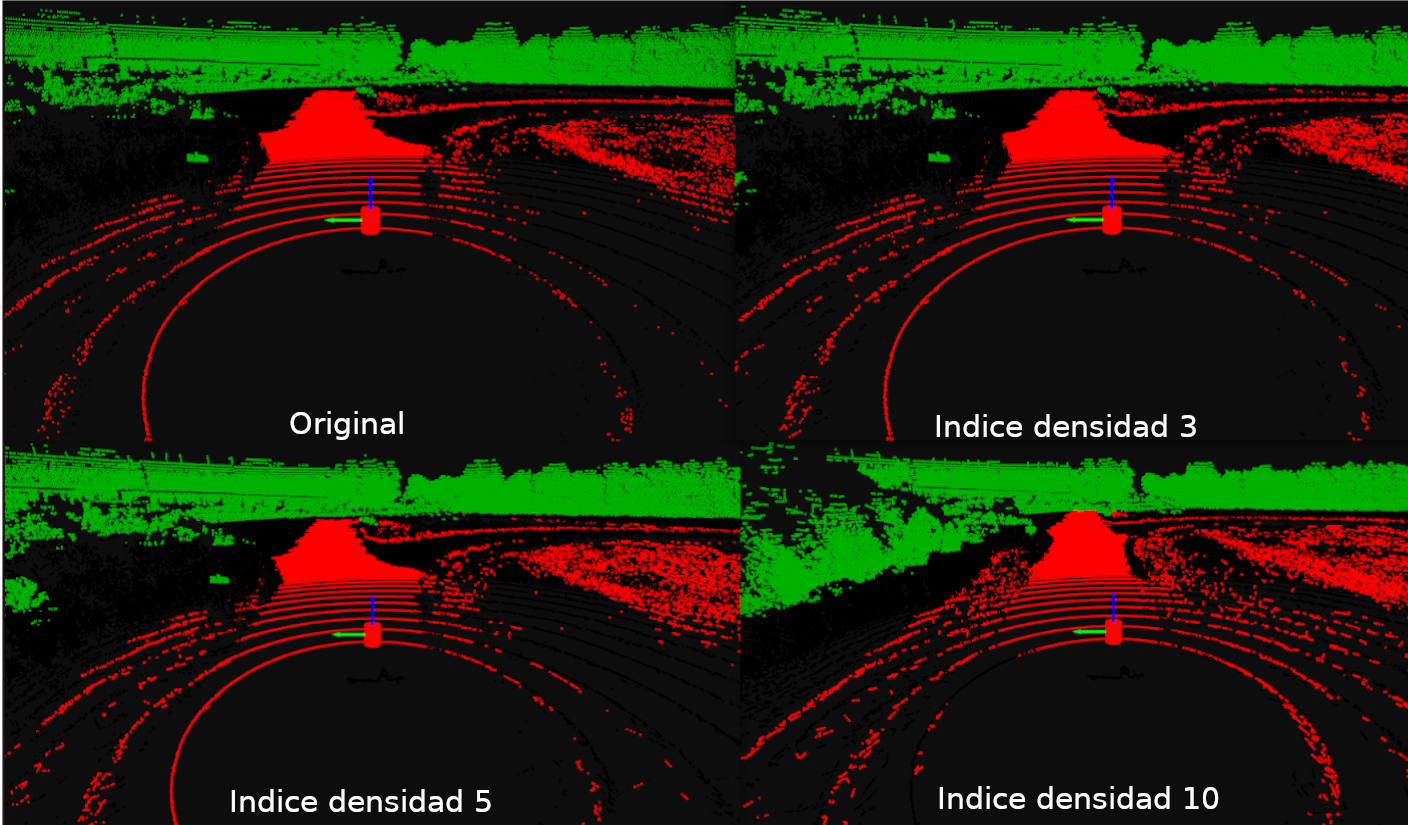
Los resultados de aplicar la densificación TIN variando el indice de densidad se muestra en la imagen siguiente:

Comparativa de la nuve de puntos tras aplicar diferentes indices de densidad.

Optimización en el método IDW

Para el algoritmo IDW, las mejoras incluyen:

• Selección vectorizada de puntos base: Mediante el uso de np.random.choize se seleccionan todos los puntos base (puntos de la nube original que se usarán para la interpolación) a la vez.

• Cálculo matricial de distancias y pesos:Se calcula simultaneamente las distnacias y pesos de interpolación.

La nueva función de densificación queda de la siguiente forma:

def densify_point_cloud(points: np.ndarray, remissions: np.ndarray, 
                                       density_factor: float = 5.0) -> Tuple[np.ndarray, np.ndarray]:
    """
    Versión vectorizada de la densificación de nubes de puntos LIDAR.
    """

    # Establecer el número de nuevos puntos a crear
    num_new_points = int((len(points) * (density_factor-1)))

    # Seleccionar puntos base de manera balanceada
    indices = np.random.choice(len(points), size=num_new_points, replace=True)


    unique_indices, counts = np.unique(indices, return_counts=True)
    point_usage_count = dict(zip(unique_indices, counts))
    
    # Encontrar vecinos más cercanos para todos los puntos seleccionados a la vez
    nn = NearestNeighbors(n_neighbors=2).fit(points)
    distances, neighbor_indices = nn.kneighbors(points[indices])


    # Los vecinos son la segunda columna (la primera es el punto mismo)
    neighbor_points = points[neighbor_indices[:, 1]]
    neighbor_remissions = remissions[neighbor_indices[:, 1]]

    #Parámetros de la distribución normal truncada
    media = 0.5
    desviacion_estandar = 0.2
    limite_inferior = 0
    limite_superior = 1   

    #Convertir los límites al espacio de la distribucion normal   
    a = (limite_inferior - media) / desviacion_estandar
    b = (limite_superior - media) / desviacion_estandar
    
    lambdas = truncnorm.rvs(a, b, loc=media, scale=desviacion_estandar, size=num_new_points)

    # Interpolación vectorizada de puntos
    base_points = points[indices]
    interpolated_points = lambdas[:, None] * base_points + (1 - lambdas[:, None]) * neighbor_points

    # Interpolación vectorizada de remisiones
    d_A = np.linalg.norm(interpolated_points - base_points, axis=1)
    d_B = np.linalg.norm(interpolated_points - neighbor_points, axis=1)


    # Evitar divisiones por cero
    d_A = np.where(d_A == 0, 1e-10, d_A)
    d_B = np.where(d_B == 0, 1e-10, d_B)
    
    w_A = 1 / d_A
    w_B = 1 / d_B

    base_remissions = remissions[indices]
    interpolated_remissions = (w_A * base_remissions + w_B * neighbor_remissions) / (w_A + w_B)


    # 6. Combinar resultados
    combined_points = np.vstack([points, interpolated_points])
    combined_remissions = np.concatenate([remissions, interpolated_remissions])

    return combined_points, combined_remissions 

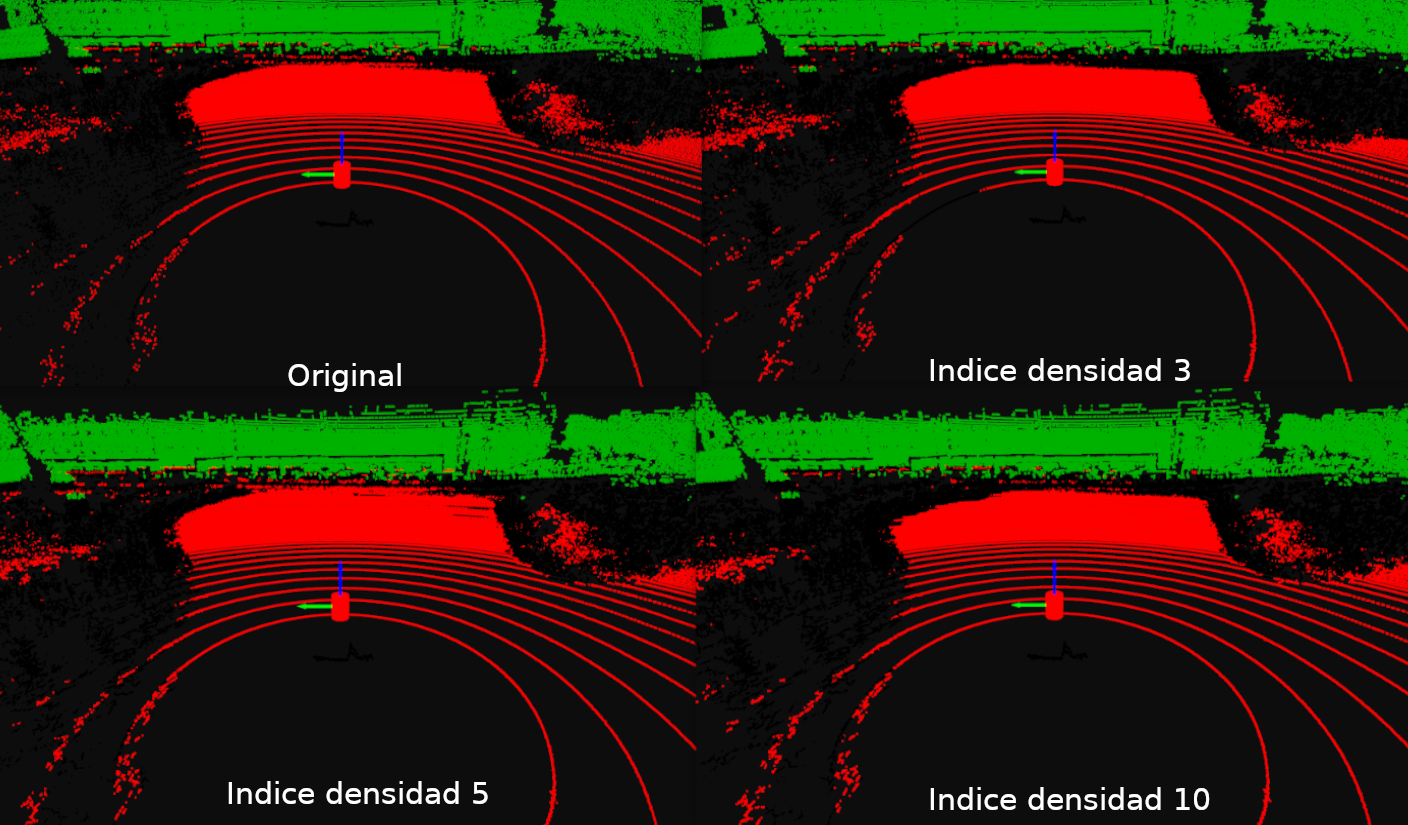
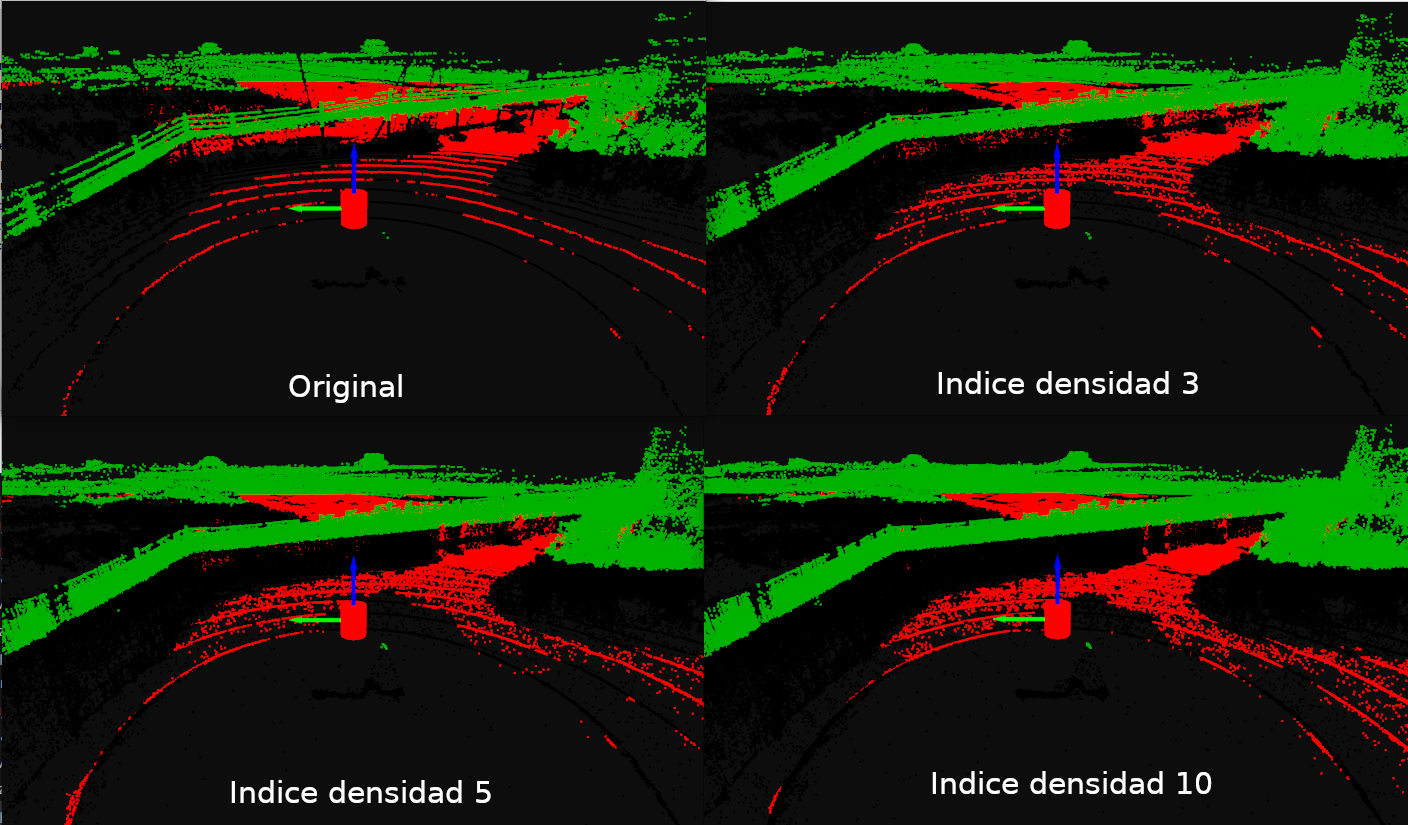
En las siguientes imágenes se muestran los resultados de aplicar IDW en las nubes de puntos de goose.

Comparativa de los resultados de aplicar IDW tomando dos vecinos y aplicar diferentes indices de densidad.

Comparativa de los resultados de aplicar IDW tomando tres vecinos y aplicar diferentes indices de densidad.