Aprendizaje por refuerzo profundo

37 minute read

Índice

Tipos de entrenamientos
Conceptos básicos RL
- Tipos de modelos RL
Q-learning
- MDP
- TD
Deep Reinforcement Learning
Gym/SB3
- Análisis de resultados

Tipos de entrenamiento

En el contexto de aprendizaje automático, existen varios tipos de entrenamiento: supervisado, no supervisado y semi-supervisados.

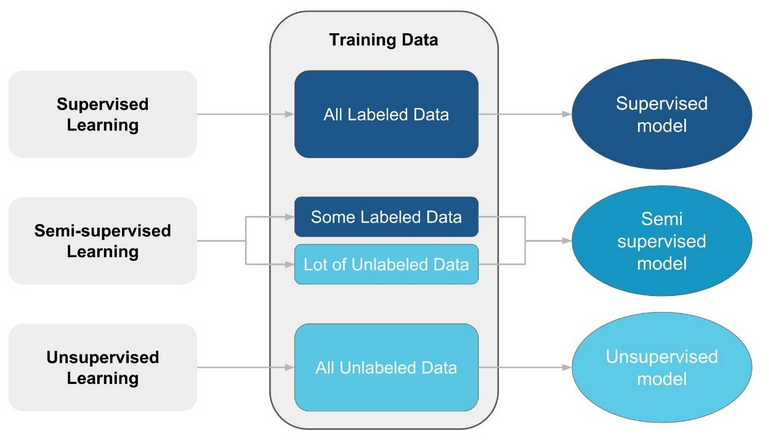
Entrenamiento supervisado

El conjunto de datos de entrenamiento es etiquetado, cada una de las entradas tiene una salida asociada a la respuesta correcta según el modelo que quiere predecir. Durante el entrenamiento, el modelo ajusta sus parámetros para minimizar el error entre las predicciones y las etiquetas reales. El objetivo de este algoritmo de aprendizaje es predecir etiquetas para datos no visto anteriormente, es ampliamente utilizado en tareas de clasificación y regresión. La precisión del modelo depende de la calidad de los datos de entrenamiento.

Entrenamiento no supervisado

El aprendizaje no supervisado opera en conjuntos de datos sin etiquetas, donde el objetivo del modelo es identificar patrones y estructuras, agrupando los datos en categorías o clústeres. Las tareas principales incluyen el clustering y la reducción de dimensionalidad. Este enfoque puede ser más rentable que el aprendizaje supervisado, ya que no requiere la creación y etiquetado de grandes conjuntos de datos de entrenamiento. En este tipo de aprendizaje, la calidad de los resultados depende en gran medida de la elección adecuada del algoritmo y los parámetros utilizados.

Entrenamiento semi-supervisado

El aprendizaje semi-supervisado emplea una combinación de datos etiquetados y no etiquetados en el conjunto de entrenamiento. Este enfoque es útil cuando el etiquetado de datos es costoso o difícil de obtener en grandes cantidades. A diferencia del aprendizaje supervisado tradicional, aquí se pueden lograr resultados significativos con solo unos pocos ejemplos etiquetados, lo que hace que el proceso sea más eficiente y práctico en ciertos escenarios. Este proceso se asemeja más a cómo aprendemos las personas.

Conceptos básicos RL

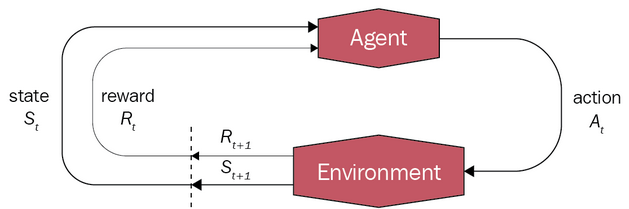
Agente: entidad que toma las decisiones.
Entorno: mundo en el que opera el agente.
Estado: donde está el agente en el entorno. Al definir los posibles estados del agente, debemos considerar qué información necesita para tomar decisiones, representada por un vector de variables relevantes. Aunque debemos tener en cuenta que algunos de estos estados pueden ser inalcanzables, por ejemplo, cuando el pasajero está en su destino pero el taxi se encuentra en cualquier otra ubicación, pero se representan todos por simplicidad.
Acción: el siguiente movimiento que va a hacer el agente. El estado en el que está el agente determina las posibles acciones a tomar, por ejemplo, un coche no puede girar a la izquierda si en ese lado hay un muro.
Recompensa: feedback que el agente recibe sobre el entorno al tomar una acción.
Valor: representa cuán bueno es tomar una acción específica en un determinado estado, este valor se calcula teniendo en cuenta las posibles recompensas futuras que el agente podría recibir y la probabilidad de alcanzar esos estados futuros.
Política: es una función que mapea los estados del agente a las acciones que debe tomar.

En un espacio de estados discreto, el éxito se define por alcanzar el estado objetivo al final de un episodio. Sin embargo, en tareas continuas, no hay un límite claro de episodios. En su lugar, el éxito se determina al mantener un conjunto específico de estados durante un período prolongado. Por ejemplo, en el caso de un péndulo, el objetivo podría ser mantener la inclinación dentro de un rango determinado durante un tiempo prolongado.

Tipos de modelos RL

Policy-based: se centra en aprender una política que maximice la recompensa, esta política es la que nos propocciona la siguiente accion (a~π(s)). Este enfoque garantiza la convergencia en una política óptima, lo que significa alcanza un punto donde se estabiliza y ya no cambia significativamente con la adición de más datos o iteraciones de entrenamiento.
Value-based: aprende una función que evalúa los pares estado-acción (Qπ(s, a)). A menudo son más eficientes en el uso de muestras que los métodos basados en política, requiere menos datos, pero no garantizan la convergencia.
Métodos combinados: prende una política encargada de seleccionar la mejor acción acciones, pero también aprenden una función de valor. Integrar la función de valor en el proceso proporciona más información a la política que solo las recompensas.
Model-based: se concentra en aprender o utilizar un modelo de las dinámicas de transición del entorno, lo que nos permitirá hacer predicciones sobre el comportamiento del mismo. Sin embargo, hacer que un modelo funcione bien con un algoritmo de RL no es trivial. Además, los modelos no siempre son conocidos, entonces necesitarán ser aprendidos, pero esto es una tarea muy difícil.

Q-learning

Q-learning es una rama del aprendizaje por refuerzo o RL (reinforcement learnin), el cual se enfoca en aprender a tomar decisiones secuenciales para maximizar una recompensa acumulativa mediante la experiencias y observaciones del entorno.

MDP

Debemos tener en cuenta que estamos en un entorno estocástico, la probabilidad del siguiente estado depende únicamente del estado actual. Matemáticamente, esto se expresa a través del proceso de decisión de Markov (MDP), que se fundamenta en las cadenas de Markov.

for episode in range(MAX_EPISODE):
  state = env.reset()
  agent.reset()

  for t in range(MAX_STEP):
    action = agent.act(state)
    state, reward = env.step(action)
    agent.update(action, state, reward)

    if env.done():
      break

TD

El algoritmo TD (Temporal Difference) combina las ventajas del algoritmo Monte Carlo, donde no es necesario conocer las dinámicas del entorno, permitiendo calcular la probabilidad de cada estado mediante la experiencia, mientras que nos sirve tanto para espacios de estados continuos como discretos. A diferencia de Monte Carlo, en TD se actualizan los valores en cada paso, no en cada episodio.

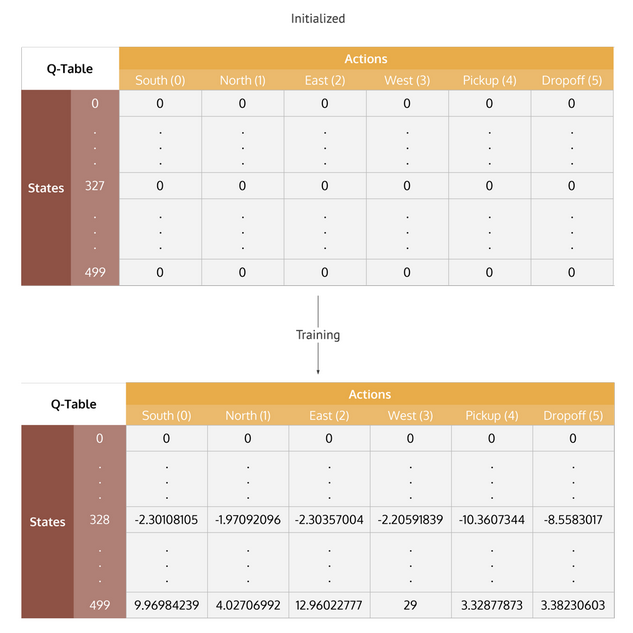
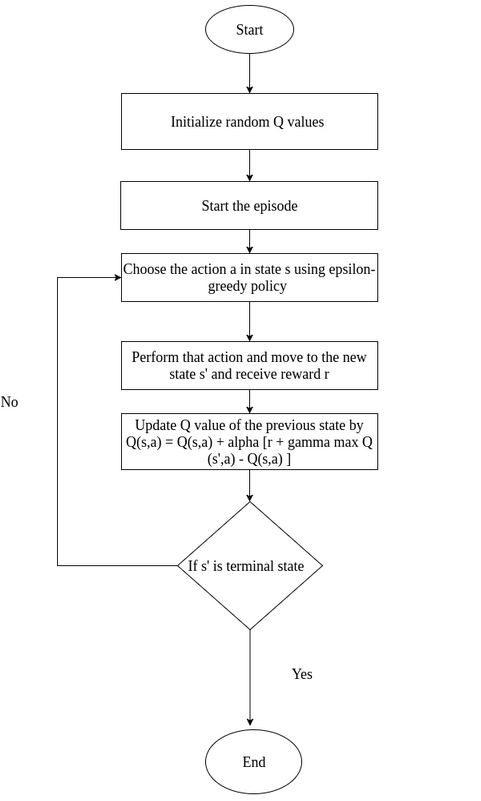
La política de un algoritmo de Q-learning se basa en los valores de una tabla que se van actualizando en cada iteración (value-based). Inicialmente, cuando el agente carece de información, la Q-table está vacía y todas las acciones tienen la misma probabilidad. Sin embargo, a medida que interactúa con el entorno, la tabla se completa y las acciones con recompensas más altas se vuelven más probables. El proceso culmina cuando la tabla converge, es decir, los valores dejan de actualizarse, momento en el que hemos encontrado la solución más óptima al problema. Por lo tanto, Q-learning es un algortimo value-based, no aprende una política como tal, se limita simplemente a escoger los valores más altos de la tabla.

La función que determina las decisiones que toma el agente es la ecuación de Bellman:

newQ(s, a) = Q(s, a) + α[R(s, a) + γ[maxQ'(s', a') - Q(s, a)]]

Donde Q(s, a) es el valor del estado actual, R(s, a) esta la recompensa recibida y maxQ’(s’, a’) es el valor máximo entre todas las posibles decisiones del agente desde el nuevo estado. El término que multiplica a γ es el error de TD, el cual debemos intentar minimizar en cada iteración.

Los hiperparámetros α, γ y ε están en el rango de 0 a 1:

Alpha: el factor de aprendizaje. Un valor de 0 indica que el agente no adquiere conocimiento (los entrenamientos serán más largos, tarda más en aprender), mientras que 1 implica entornos deterministas. La reducción gradual de α a lo largo del tiempo previene el overfitting.
Gamma: el factor de descuento, que determina cómo el agente valora las recompensas futuras en relación con las inmediatas. Un valor de gamma cercano a 1 significa que el agente valora mucho las recompensas futuras, mientras que un valor cercano a 0 indica que se enfoca principalmente en las recompensas inmediatas. A medida que nos acercamos al objetivo, es preferible aprovechar las recompensas a corto plazo en lugar de esperar por las futuras, que pueden no estar disponibles una vez que se complete la tarea.
Epsilon: el ratio de exploración. Al principio, el agente debe explorar diferentes acciones para encontrar las que producen mayor recompensa, pero con el tiempo, debe priorizar la explotación de las mejores acciones. Reducir ε con el tiempo nos permite conseguir este enfoque y que la Q-table converja de manera óptima. Esta estrategia se conoce como política ε-greedy:

epsilon = 0.3
epsilon_decay = 0.99  # decreasing by 1% each time

if epsilon < threshold:
  explore()
else:
  exploit()

epsilon = epsilon * epsilon_decay

En este diagrama, se presenta la definición completa del algoritmo:

Deep Reinforcement Learning

El aprendizaje profundo aplicado al aprendizaje por refuerzo permite a los agentes manejar entornos con espacios de estados complejo donde el mapeo de valores no es lineal. Sin embargo, usar aprendizaje profundo en RL es más desafiante que en el aprendizaje supervisado, ya que los agentes a menudo deben esperar mucho tiempo para recibir retroalimentación.

En el ámbito de los algoritmos de deep RL, debemos distinguir entre dos tipos:

On-policy: son aquellos que actualizan el modelo solo con datos de la política actual, una vez que la política cambia, los datos anteriores se vuelven inservibles y se descartan.
Off-policy: pueden usar cualquier dato recolectado durante el entrenamiento, independientemente de la política con la que hayan sido obtenidos.

Para entrenar modelos de deep RL utilizaremos la librería de Python *stable_baselines3, ya que facilita la experimentación con diferentes algoritmos y configuraciones.

DQN

Al igual que el algotirmo Q-learning, DQN es un modelo value-based y además es un algoritmo off-policy, no solo utiliza datos basados en la política actual, como veremos en el aparatdo de replay memory.

Una Q-table ya no es una forma práctica de modelar la función de transición de estado-acción, especialmente cuando el espacio de estados es muy extenso o continuo, debido a que requeriríamos explorar cada estado al menos una vez para encontrar la mejor solución. En su lugar, utilizaremos una Q-network, que es un tipo de red neuronal diseñada para aproximar los Q-values, es decir, aprende la función que mapea estados-acciones (Q-function). Esta red es capaz de estimar el Q-value de estados no explorados, ya que aprende las relaciones entre los diferentes pares estado-acción.

En una Q-table, almacenamos los valores en una tabla, mientras que en una Q-network, esta información se guarda en los pesos de la red, los cuales actúan como coeficientes en la Q-function. Una Q-network recibe los estados del entorno como entrada y produce como salida el Q-value de cada acción posible. También incluye una función de pérdida que evalúa la diferencia entre los Q-values predichos y reales, y se utiliza para actualizar los pesos de la red mediante retropropagación.

Política Boltzmann

Como ya vimos con anterioridad en el aparatdo de ε-greedy, necesitamos un balance entre explotación y explotación. Esta técnica explora de manera aleatoria, con Boltzman pretendemos explorar con un mayor grado de conocimeinto, las acciones de q-values mas altos tienenn mas probabilidad de ser elegidas. Para ello utilizamos la función softmax parametrizada por τ , valores altos de τ definen una distribución más uniforme, las acciones tienen probabilidades más parecidas, se elige de manera mas aleatoria; mientras que valotes de τ bajos, hacen que la seleccion se concrente en los q values altos.

pboltzmann(a | s) = exp(Q(s, a) / τ) / Σ(exp(Q(s, a') / τ))

Como ya discutimos en el apartado de ε-greedy, necesitamos encontrar un equilibrio entre la exploración y la explotación. Mientras que la técnica ε-greedy es totalmente aleatoria en la exploración y en explotación utiliza argmax, la política de Boltzmann busca explorar con un mayor grado de conocimiento. En esta estrategia, las acciones con Q-vañues más altos tienen una probabilidad más alta de ser seleccionadas, para lograrlo, empleamos la función softmax parametrizada por τ. Cuando τ es alto, se obtiene una distribución de probabilidad más uniforme, lo que significa que todas las acciones tienen probabilidades similares de ser seleccionadas, lo que resulta en una exploración más aleatoria. Por otro lado, cuando τ es bajo, la selección se concentra en las acciones con Q-values más altos, lo que lleva a una mayor explotación de estas acciones.

τ = 1 -> p(x) = [0.27, 0.73] (softmax)

τ = 5 -> p(x) = [0.45, 0.55]

τ = 0.5 -> p(x) = [0.12, 0.88]

La política de Boltzmann también ofrece una relación más suave entre las estimaciones de los Q-values y las probabilidades de acción en comparación con una política ε-greedy. Por ejemplo, si consideramos dos posibles acciones con Q-values de Q(s, a1) = 5.05 y Q(s, a2) = 4.95, con la política ε-greedy, a2 tendría casi toda la probabilidad de ser elegida, mientras que con la política de Boltzmann, ambas acciones tendrían probabilidades muy similares.

Sin embargo, la política de Boltzmann tiene el riesgo de quedarse atrapada en un mínimo local. Por ejemplo, si tenemos Q(s, a1) = 2.5 y Q(s, a2) = -3, y a2 es la mejor opción, a pesar de ello, a2 tendría una probabilidad extremadamente baja de ser seleccionada con la política de Boltzmann, mientras que con la política ε-greedy esta probabilidad no sería tan pequeña. Este problema puede abordarse disminuyendo gradualmente el parámetro τ, pero debemos tener cuidado de no reducirlo demasiado rápido, ya que podríamos seguir quedando atrapados en mínimos locales.

Experience replay

Esta técnica consiste en crear una memoria de reproducción de experiencias que almacena las k experiencias más recientes que un agente ha recopilado, ya que son las más relevantes, para así poder reutilizarlas. Si la memoria está llena, se descarta la experiencia más antigua para dar espacio a la más reciente. En cada paso de entrenamiento, se muestrea uno o más lotes de datos de forma aleatoria desde la memoria para actualizar los parámetros de la red. El valor de k suele ser bastante grande, entre 10,000 y 1,000,000, mientras que el número de elementos en un lote es mucho más pequeño, típicamente entre 32 y 2048.

El tamaño de la memoria debe ser lo suficientemente grande como para contener muchas experiencias de episodios. Cada lote típicamente contendrá experiencias de diferentes episodios y diferentes políticas, lo que descorrelaciona las experiencias utilizadas para entrenar a un agente. Esto, a su vez, reduce la varianza de las actualizaciones de parámetros, lo que ayuda a estabilizar el entrenamiento. No obstante, la memoria también debe ser lo suficientemente pequeña como para que cada experiencia tenga más probabilidades de ser muestreada más de una vez antes de ser descartada, lo que hace que el aprendizaje sea más eficiente.

El hiperparámetro learning_starts define el número de pasos previos antes de que comience el proceso de aprendizaje efectivo. Durante estos pasos iniciales, las experiencias se almacenan en la memoria, pero la red neuronal no se actualiza.

Target network

La red principal, policy network (θ), se actualiza en cada paso de entrenamiento, lo que dificulta la minimización del error entre las predicciones de la red y los valores reales. Para abordar este problema, introducimos una nueva red neural, target network (φ), diseñada para aportar estabilidad al proceso de entrenamiento. La target network es una réplica de la red original, pero en lugar de actualizarla en cada paso, la igualamos a la policy network cada cierto número de pasos determinado (F), generalmente entre 100 y 1000. Utilizamos esta red para calcular los Q-values, ya que mantiene un objetivo de entrenamiento constante. Sin embargo, una desventaja es que puede ralentizar el entrenamiento, ya que se basa en una versión anterior de la red.

También está la actualización Polyak, donde actualizamos φ en cada paso mediante una mezcla de los parámetros de ambas redes. El hiperparámetro β controla la velocidad del cambio en φ, siendo más lento cuanto mayor sea β. Si φ y θ están muy próximos, el entrenamiento puede volverse inestable. Por otro lado, si φ cambia demasiado lentamente, el proceso de entrenamiento puede ser lento, como en la técnica anterior.

φ = φ * (1 - β) + θ * β

Doble DQN

El algoritmo original de DQN tiende a sobreestimar los Q-values para los pares estado-acción más frecuentemente visitados, lo que puede resultar en problemas si la exploración del entorno no es uniforme. Esta sobreestimación se manifiesta en los valores sesgados positivamente que obtenemos en la función maxQ(s’, a’). Además, cuanto mayor sea el número de acciones posibles, mayor será el error introducido. Estos errores se propagan hacia atrás a través de toda la red.

Para abordar este problema, la acción que maximiza la recompensa se obtiene con la red original θ, mientras que el Q-value se estima con la red φ. Al utilizar una segunda Q-function entrenada con experiencias diferentes, se elimina el sesgo positivo en la estimación. Esta técnica mejora la convergencia y la estabilidad del entrenamiento.

a' = max[Q_θ(s', a')] y = r + γ * max[Q_φ(s', a')]

PER

El Prioritized Experience Replay (PER) es una estrategia que implica seleccionar con mayor frecuencia las experiencias de la memoriaque aportan una mayor información, en lugar de hacerlo de forma aleatoria. Este enfoque acelera y mejora la eficiencia del entrenamiento. La prioridad de cada experiencia se puede inferir del error TD (ωi) mediante el método de priorización proporcional, garantizando que las experiencias con puntuaciones más altas se seleccionen con mayor frecuencia y que cada experiencia tiene una probabilidad no nula de ser seleccionada. ε es un número positivo pequeño (para asegurar que ωi no sea igual a cero) y η ∈ [0, ∞), un valor mayor de η aumenta la de prioridad de las experiencias más relevantes.

p[i] = (|ωi| + ε)ᵞ / Σ(|ωj| + ε)ᵞ

η = 0.0: (ω1 = 2.0, ω2 = 3.5) => (P(1) = 0.5, P(2) = 0.5)

η = 1.0: (ω1 = 2.0, ω2 = 3.5) => (P(1) = 0.36, P(2) = 0.64)

Algoritmo DQN

s = env.reset()

for m in range(MAX_STEPS): # Número de pasos (interacciones con el entorno)
  a = θ.predict(s) # Seleccionar una acción según la política actual
  r, s_next, finish = env.step(a) # Ejecutar la acción
  b.append([s, a, r, s_next]) # Guardamos la nueva experiencia

  for b in range(B): # Número de lotes por step
    b = get_random_batch() # Obtener los lotes

    for u in range(U): # Actualizaciones por lote
      for i in range(N): # Número de experiencias por lote
        si, ai, ri, s_next_i = b[i]
        y = ri + γ * max(Qφ(s_next, max(Qθ(s_next_i, a_next)))) 
        w[i] = abs(y - Qθ(si, ai)) # Error TD

      L(θ) = 1 / N * sum(w ** 2) # Función de pérdida
      θ = θ + α * ∇θ * L(θ) # Actualizar los pesos de la red principal
      p = [(w[i] + ε) ** η / sum((w + ε) ** η) for i in range(N)]  # Calcular la prioridad de cada experiencia
      
  # Actualizar estado
  if finish:
    s = env.reset() # Termina un episodio
  else:
    s = s_next 

  # Política Boltzmann
  τ  = τ * decay_factor_τ

  if m % F == 0: # Actualizar Target network
    φ = θ

Unos valores óptimos para los parámetros U y B dependen del problema y de los recursos computacionales disponibles, sin embargo, son comunes valores en el rango de 1 a 5. Debemos resaltar que, para calcular el siguiente estado, es necesario seleccionar el valor máximo entre tod as las posibles acciones del estado siguiente, por lo tanto, el espacio de acciones debe ser discreto.

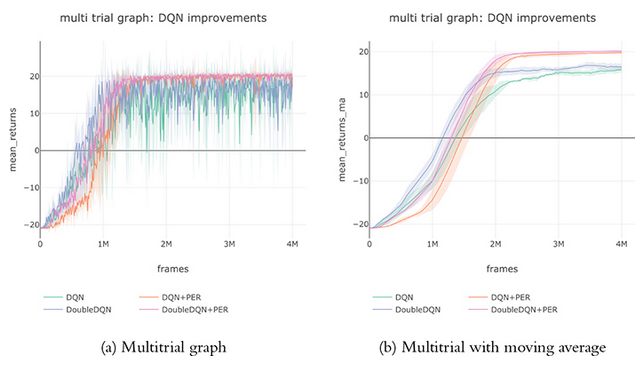
Aquí podemos observar una gráfica comparativa entre DQN y la incorporación de las mejoras que hemos ido añadiendo. Moving Average es una técnica utilizada para suavizar la curva de recompensa y facilitar una mejor evaluación de su tendencia. Para ello, calcula el promedio de las recompensas de las últimas n acciones más recientes, eliminando fluctuaciones aleatorias y ruido.

Actor-Critic algorithms: A2C

El algoritmo Actor-Critic es un tipo de algortimo de gradiente por política (PG). Cada agente consta de dos elementos que aprenden de manera conjunta, cada uno con su propia red neuronal: actor (θA), encargado de aprender la política óptima (π), y el critic (θC), responsable de aprender la función de valor (Q) y proporcionar una señal de refuerzo a la política.

Actor

El actor se fundamenta en el algoritmo REINFORCE, donde se busca aprender una política parametrizada (π_θ, con θ como la red neuronal que parametriza la política π) con el objetivo de maximizar la recompensa final. Para actualizar los parámetros de la política, en REINFORCE se utilizaba la estimación de Monte Carlo, pero ahora emplearemos la función de ventaja.

Función objetivo: J(π_θ) = E_t[A^π_θ_t] (E = esperanza)
Para maximizar esta función objetivo, aplicamos la técnica de ascenso por gradiente: ∇J(π_θ) = E_t[A^π_θ_t * ∇_θ * log(π_θ(a_t | s_t))]
Actualización de parámetros: θ = θ + α∇_θJ(π_θ)

Critic

Para elegir la siguiente acción usaremos la función de ventaja (A), la cual no se basa únicamente en la función de valor (Q), sino que se combina con el valor promedio de las acciones en el estado actual (V), de esta manera, la ventaja nos cuantifica cuánto mejor o peor es la acción tomda respecto a la media.

A^π(s, a) = Q^π(s, a) - V^π(s)

El crtic es el encargado de aprender a evaluar los pares (s, a) y utilizar esta evaluación para generar A^π. A continuación, exploraremos dos técnicas para estimar la función de ventaja: n-steps returns y GAE.

N-steps returns

Consiste en aprender Q^π y V^π con dos redes neuronales diferentes, pero debemos asegurarnos de que ambas sean consistentes. Este enfoque es poco eficiente, por ello, se suele aprender solo V^π y combinarla con una trayectoria de recompensas (r1 + r2 + r3 + … + rn) para estimar Q^π. Aprendemos V^π en vez de Q^π porque es menos complejo, requiere menos muestras, y es problemático cuando el actor y el critic aprenden de manera simultánea. Además, como estamos estimando Q^π, podemos tener un espacio de acciones continuo, a diferencia que DQN.

La función de valor puede expresarse como una combinación de las recompensas esperadas para n pasos de tiempo, seguida por una predicción de la media. Si n tiene un valor grande, podemos introducir una alta varianza en la estimación, lo que la hace menos fiable. Sin embargo, si n es muy bajo, no estamos considerando suficientes pasos y las estimaciones pueden estar sesgadas (diferencia entre el valor obtenido y el valor real). γ es el factor de descuento que vimos en apartados anteriores.

Q^π(s_t, a_t) ≈ r_t + γ r_{t + 1} + γ² r_{t + 2} + … + γⁿ r_{t + n} + V^π(s_{t + n + 1})

A_NSTEP^π(s_t, a_t) = Q^π(s_t, a_t) − V^π(s _t) ≈ r_t + γ r_{t + 1} + γ² r_{t + 2} + … + γⁿ r_{t + n} + γ^{n + 1} V^π(s_{t + n + 1}) − V^π(s_t)

GAE

Generalized Advantage Estimation (GAE) se crea con el objetivo de reducir la varianza y mantener un sesgo bajo, calculamos una media ponderada de múltiples estimadores de ventaja que varían desde n = 1 hasta k. La contribución decae exponencialmente con una tasa controlada por el parámetro λ (gae_lambda) Un valor alto de λ reduce la varianza, ya que se basa en la combinación de más pasos futuros, reduciendo el impacto de fluctuaciones momentaneas en la recompensa, se puede decir que la informacion e smas gental. Un valor alto de λ reduce la varianza, ya que la estimación de la ventaja se basa en la combinación de más pasos futuros, lo que disminuye el impacto de las fluctuaciones momentáneas en las recompensas y proporciona una perspectiva más general. Sin embargo, esto puede introducir un mayor sesgo, ya que las estimaciones basadas en el futuro tienden a ser menos precisas que las observaciones inmediatas.

δ_t = r_t + γ V^π(s_{t + 1}) − V^π(s_t) -> Es la ecuación para 1-step

A_t^π(1) = δ_t At_t^π(2) = δ_t + γ δ_{t + 1} At_t^π(3) = δ_t + γ δ_{t + 1} + γ² δ_{t + 2}

A_GAE^π(s_t, a_t) = ∑_ℓ=0^∞(γλ)^ℓ δ_t+ℓ

En estas dos técnicas, asumimos que tenemos acceso a V^π para realizar predicciones. Para actualizar θc utilizaremos la misma técnica que en DQN: calcular el error cuadrático medio (MSE) entre la predicción y el valor objetivo. Existen varias formas de calcular este valor objetivo (target), que normalmente depende del método utilizado para calcular la función de ventaja.

V_tar^π(s) = r + V^π(s’; θ) = r_t + γ r_{t + 1} + γ² r_{t + 2} + … + γⁿ r_{t + n} + V^π(s_{t + n + 1}) (n-steps)
Monte Carlo: V_tar^π(s) = A_GAE^π(s_t, a_t) + V^π(s_t) (GAE)

Algoritmo A2C

El algoritmo Advantage Actor-Critic (A2C) se forma a partir de la unión del actor y el critic y es una algoritmo on-policy. Este algoritmo muestra entrenamiento episódico, pero este enfoque también se puede aplicar al entrenamiento por lotes.

init(αA, αC, β, θA, θC)

for r in range(MAX_EPISODES):
  a, s, r, s_next = env.exec(θA) # Actuar en el entorno según la política actual

  for t in range(T): # Número de pasos
    V_pred[t] = θC.predict(s[t])
    A_pred[t] = θC.predict(s[t], a[t])
    V_tar[t] = θC.predict_target(s) # Depende del método también puede necesitarse la trayectoria de recompensas
    H[t] = θA.entropy() # Calculamos la entropía

  # Calculamos las funciones de pérdida
  Lval(θC) = [1/T * sum((V_pred[t] - V_tar()) ** 2) for t in range(T)]
  # El signo menos es porque queremos maximizar el gradiente
  Lpol(θA) = [1/T * sum(-A_pred[t] * logπθA(a[t]|s[t]) - β * H[t]) for t in range(T)] 

  # Actualizar los parámetros de las redes
  θC = θC + αC * ∇θC * Lval(θC)
  θA = θA + αA * ∇θA * Lpol(θA)

El propósito de regular la entropía es promover la exploración. Las políticas menos uniformes generan acciones similares con menor entropía (explotación), mientras que las políticas uniformes conducen a acciones más diversas (exploración). El parámetro β controla el peso de la entropía en el cálculo de la función de pérdida. Tanto la entropía H como β son siempre valores no negativos, lo que hace que −βH sea negativo. Cuando una política es menos uniforme, la entropía disminuye, lo que aumenta −βH y su contribución a la pérdida, fomentando así que la política se vuelva más uniforme. De lo contrario, esto apenas tiene impacto en el cálculo cuando la política es uniforme.

La tasa de aprendizaje del actor debe ser más pequeña y reducirse a cero más rápido que la del crítico. Esta observación es crucial para la estabilidad del aprendizaje. Si la política de comportamiento es demasiado inestable, las trayectorias generadas serán demasiado erráticas, lo que dificultará que la política objetivo aprenda de manera efectiva. Al mantener la política de comportamiento más estable, se proporciona un entorno más consistente para que la política objetivo pueda aprender y ajustarse de manera eficiente.

Arquitectura de la red neuronal

Si separamos las redes del actor y critic, es probable que el actor no adquiera conocimientos útiles hasta que el critic se vuelva más razonable, lo que podría requerir numerosas etapas de entrenamiento. Sin embargo, si comparten parámetros, el actor puede beneficiarse de la representación del estado que está siendo aprendida por el critic. Lo más habitual es que compartan las capas del nivel inferior, pero no las del superior, dado que tienen diferentes salidas: para el actor, es una distribución de probabilidad sobre acciones, mientras que para el critic, es un único valor escalar que representa V^π(s). No obstante, esto conlleva el riesgo de volver el aprendizaje inestable, ya que ahora hay dos componentes del gradiente que se propagan hacia atrás y pueden tener escalas muy diferentes.

Paralelización de métodos

En los algoritmos on-policy, no contamos con una memoria de experiencias que diversifique el entrenamiento. En su lugar, las experiencias son consecutivas y, por lo tanto, están relacionadas, lo que ralentiza el proceso de aprendizaje. Para mejorar la eficiencia, se paralelizan el agente y el entorno creando múltiples instancias idénticas para recopilar trayectorias de manera independiente entre sí. Dado que un agente está parametrizado por una red, creamos múltiples redes de trabajo idénticas y una red global. Los trabajadores recopilan trayectorias de forma continua, y la red global se actualiza periódicamente utilizando datos de los trabajadores antes de devolver los cambios a los trabajadores.

Esta paralelización puede realizarse de manera síncrona o asíncrona. En la sincronización, la red global espera a recibir actualizaciones de todos los trabajadores, luego los trabajadores esperan a que la red global se actualice y envíe los nuevos parámetros. En contraste, en la asincronización, la red global actualiza sus parámetros cada vez que recibe una actualización de cualquier trabajador, mientras que los trabajadores se actualizan desde la red global periódicamente. Esto implica que las diferentes redes tengan ligeras variaciones en sus parámetros.

PPO

PPO (Proximal Policy Optimization) es un algoritmo on-policy que puede considerarse como una extensión de A2C. Su objetivo principal es abordar dos problemas fundamentales:

Evitar el deterioro del rendimiento: en los algoritmos basados en políticas, ajustar el parámetro α puede ser complicado. Un valor pequeño puede llevar a entrenamientos prolongados sin alcanzar la solución óptima, mientras que uno grande puede causar un colapso en el rendimiento. Para resolver esto, PPO introduce un objetivo sustituto que asegura una mejora monótona del rendimiento.
Reutilización eficiente de datos: establecer este objetivo sustituto, también promueve la reutilización de datos fuera de la política.

Objetivo sustituido

PPO utiliza la diferencia relativa de rendimiento entre políticas (δ) durante la optimización, se garantiza que esta diferencia sea no negativa en cada iteración, asegurando así una mejora continua en el rendimiento, y que no sea excesivamnete grande (δ_tar: valor objetivo), introdución una restricción en el tamño del paso.

Sin embargo, surge un problema porque las trayectorias deben ser muestreadas con la nueva política, que no está disponible hasta después de la actualización. Para abordar esto, se utilizan pesos de muestreo por importancia para aproximar las trayectorias con la política anterior, esto ajusta las recompensas asociadas con las acciones de manera que las acciones más probables bajo la nueva política se vean reforzadas, mientras que las menos probables se reduzcan. Este enfoque asegura que la optimización siga siendo efectiva bajo el proceso de ascenso por gradiente.

Finalmente, el objetivo sustituido se describe mediante la siguiente fórmula:

J^CIP = r_t(θ) * A_t

Variantes

La variante de PPO con penalización KL adaptativa, KL es una medida de la diferencia entre dos distribuciones de probabilidad, usada para regular el cambio permitido entre politicas. En esta variante, el objetivo sustituido penalizado por KL está regulado por un coeficiente adaptativo β, que controla el peso de la penalización KL. Un valor mayor de β permite una mayor diferencia entre π_θ y π_θold, mientras que un valor menor de β reduce la tolerancia entre las dos políticas. Debido a la dificultad de fijar un valor constante para este parámetro que funcione en todas las situaciones, se propone actualizar su valor en cada iteración:

if δ < δtar / 1.5 :
  β /=2
else if δ > δtar * 1.5:
  β *=2

Este enfoque tiene la ventaja de ser simple de implementar. Sin embargo, no resuelve el problema de elegir un δ objetivo o el margen de actualización, que son problemas complejos. Además, puede ser computacionalmente costoso debido a la necesidad de calcular la divergencia KL.

J^KLPEN(θ) = max_θ E_t[r_t(θ) * A_t − β KL(π_θ(a_t ∣ s_t) ∣∣ π_{θ_old}(a_t ∣ s_t))]

Para solucionar estos problemas, sea creó la variante PPO con objetivo sustituido clipped, que calcula dicho objetivo de manera simplificada.

J^CLIP(θ) = E_t[min(r_t(θ) * A_t, clip(r_t(θ), 1−ϵ, 1+ϵ) * A_t)], donde r_t es la relación de probabilidades entre políticas

ϵ es el hiperparámetro que define el vecindario de recorte, limita el valor de J^CPI entre [(1−ϵ)At_t y (1+ϵ)A_t]. Cuando r_t(θ) está dentro del intervalo [1−ϵ, 1+ϵ], ambos términos dentro del min⁡(⋅) son iguales. Es recomendable que le valor de ϵ decaiga a medida que avanza el entrenamiento. Este objetivo previene actualizaciones de parámetros que podrían causar cambios grandes y arriesgados en la política. Además, los cálculos son mucho menos costosos que los de la técnica anterior y obtienen un mejor rendimiento, por lo que generalmente es la estrategia utilizada.

Algoritmo PPO clipping

batch = [[experiences], [A], [V_tar]]

while not finish: # El entrenamiento se ejecuta hasta que se alcanza un crítico de parada
  θAold = θA
  
  for t in range(T): # Time steps
    batch[t, 0] = θAold.step() # trayectoria
    batch[t, 1] = θAold.advantage() # A (ventaja)
    batch[t, 2]= θC.mean_tar(trayectory) # V_tar

  for epoch in range(K): # Número de actualizaciones
    for mini_batch in range(0, T, M): # M <= T -> tamaño del minibatch
      r = θA.relation(mini_batch) # Calculamos la relación entre políticas 
      J_clip = θA.caculate_Jclip(Am, r) # Am se extraer del mini lote
      H = θA.entropy(mini_batch)

      # Calcular las funciones de pérdida
      Lpol(θA) = J_clip(θA) - β * H
      V_pred = θC.predict(sm) # sm se extrae de las experiencias del mini lote
      Lval(θC) = MSE(V_pred, V_tar_m) # V_tar se extrae del mini lote

      # Actualizar los parámetros de las redes
      θC = θC + αC * ∇θC * Lval(θC)
      θA = θA + αA * ∇θA * Lpol(θA)

DDPG

Los algoritmos de gradiente de política off-policy son prometedores porque permiten que el actor se concentre en la exploración y que el critic se entrene de manera offline, aun que presenta un desafío importante para la estabilidad y la convergencia. El actor, al utilizar la política de comportamiento, aún necesita maximizar sobre todas las acciones para seleccionar la mejor trayectoria, lo cual podría volverse computacionalmente problemático. En su lugar, se propone ir moviendo la política de comportamiento hacia mejores acciones basadas en las estimaciones actuales, esto se conoce como DPG (Deterministic Policy Gradients). DPG no produce probabilidades de acción y, por ende, carece de un mecanismo natural de exploración; si el agente tiene éxito, seguirá obteniendo la misma trayectoria una y otra vez. En el caso de DPG, el objetivo incluye una función determinista, no una política estocástica como en los algoritmos PG tradicionales.

DDPG puede resolver aproximaciones no lineales y modelos más complejos, mejorando la convergencia en comparación con DPG. Su popularidad se debe a que puede manejar tanto espacios de estado complejos y de alta dimensión como espacios de acción continuos y de alta dimensión (no maneja espacios de acciones discreto). Los algoritmos anteriores complicaban las matemáticas porque mezclan el cálculo del gradiente en el propio algoritmo. DDPG delega la optimización del actor/critic en el marco de aprendizaje profundo. Además, permite usar ruido en la predicción de acciones para estimular la exploración, lo cual es más eficinete que agregar ruido directamente en la acción.

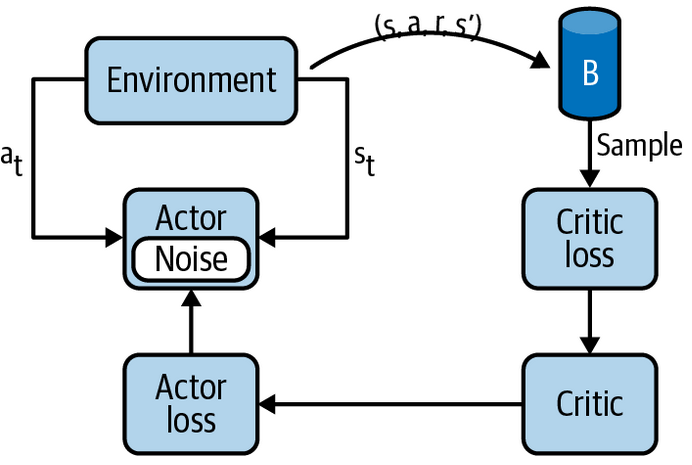
Basado en el esquema anterior, el algoritmo DDPG se define de la siguiente manera:

for episode in range(MAX_EPISODES):
  s = env.reset()

  while not terminated:
    a = θA.predict(s) + noise
    r, s_next, terminated = env.step(a)
    b.append([s, a, r, s_next]) # Guardamos la experiencia en el replay buffer

    for i in range(N): # Número de experiencias por lote
      s[i], a[i], ri, s_next_i = b[i]
      y[i] = ri + γ * (φC(s_next_i, φA(s_next_i))) # Usamos las target networks

    # Actualización del actor y el critic
    θC = θC + αC * (1/N * sum((y[i] - θC(s[i], a[i]))**2))
    θA = θA + αA * (1/N * sum((∇θA * θC(s[i], a[i]))**2))

    # Actuacización de target networks
    φA = φA * (1 - β) + θA * β
    φC = φC * (1 - β) + θC * β

    s = s_next

Este algoritmo se considera difícil de usar por su extrema fragilidad y sensibilidad a los hiperparámetro.

TD3

Twin delay DDPG o TD3 introduce tres nuevas actualizaciones con respecto a DDPG que mejoran notablemente la robustez y el rendimiento:

DPU (delay policy updates): retrasa la actualización de la política (actor) y las target networks, actualizándolas cada d iteraciones. Esta técnica “espera para evaluar la efectividad de las acciones”, lo que mejora el rendimiento significativamente.
CDQ (Clipped double Q-learning): utiliza dos redes critic con pesos diferentes, pero en arquitecturas profundas esta estrategia puede no ser óptima. La solución más simple y efectiva es elegir la estimación de valor de acción más baja entre las dos durante el entrenamiento. Esta táctica previene la sobreestimación de acciones, por ejemplo, es efectiva en entornos donde se valora una mayor estabilidad, algo que no depende exclusivamente de acciones individuales.
TPS (Target policy smoothing): agrega ruido a las acciones dentro de un rango [-c, c] para suavizar picos, permitiendo una adaptación más flexible a nuevas y mejores estrategias. Esta mejora tiene un impacto menos marcado en el rendimiento, pero contribuye a la estabilidad del entrenamiento.

El algoritmo TD3 es muy similar al DDPG, pero incorporando las mejoras mencionadas.

θA, θC1, θC2 # networks
φA, φC1, φC2 # target networks

for episode in range(MAX_EPISODES):
  s = env.reset()
  t = 0

  while not terminated:
    a = θA.predict(s) + noise
    r, s_next, terminated = env.step(a)
    b.append([s, a, r, s_next]) 

    for i in range(N): 
      s[i], a[i], ri, s_next_i = b[i]
      a_smooth = φA.predict(s_next_i) + clip(noise, -c, c) # TPS -> se calcula con la target network del actor
      y[i] = ri + γ * min(φC1(s_next_i, a_smooth), φC2(s_next_i, a_smooth)) # CDQ

    # Actualizar los critics
    θC1 = θC1 + αC * (1/N * sum((y[i] - θC1(s[i], a[i]))**2))
    θC2 = θC2 + αC * (1/N * sum((y[i] - θC2(s[i], a[i]))**2))

    if t % d == 0: # DPU
      θA = θA + αA * (1/N * sum((∇θA * θC(s[i], a[i]))**2))

      φA = φA * (1 - β) + θA * β
      φC = φC * (1 - β) + θC * β

    s = s_next
    t += 1

SAC

El término soft indica que el objetivo del algoritmo es maximizar la entropía. La entropía representa la cantidad de información contenida en una variable estocástica. Por ejemplo, en el caso de una moneda con dos estados, la información se puede medir como el número de bits necesarios para codificar esos estados (0 o 1, solo se necesita un bit). Maximizar la entropía de una política impulsa al agente a explorar todos los estados y acciones posibles, forzando al agente a aprender todas las formas de resolver la tarea.

Función que maximiza la recompensa: J(π) = E_π\[∑_t=0T(r_t + β * H(π(⋅∣s_t)))\]

Si estamos un problema discretizado que solo tiene una trayectoria óptima y nunca esperas que el agente se desvíe de esa trayectoria, entonces una política determinista es una buena opción, DDPG o TD3. Sin embargo, en problemas continuos o de alta dimensionalidad, donde es probable que el agente se desvíe de la política óptima, una política estocástica podría ser preferible. Esta opción fomenta una exploración variada y robusta, lo cual puede mejorar el rendimiento y la estabilidad del agente.

En un modelo SAC (Soft Actor Critic), el actor tiene como objetivo maximizar tanto la recompensa esperada como la entropía. Esto significa que el objetivo es tener éxito en la tarea actuando de la manera más aleatoria posible. El hiperparámetro β permite controlar cuánto influye la entropía en los cálculos; valores cercanos a cero hacen que el comportamiento sea más determinista, mientras que valores más altos promueven acciones no deterministas y, por lo tanto, mayor exploración. Este modelo es muy sensible a este parámetro y está diseñado para espacios de acciones continuos y no funciona directamente para espacios discretos.

Funciones que difieren de los modelos deterministas anteriores:

state-value function: V(s) = E\[Q(s, a) + β * H(π(a∣s))\] = E\[Q(s, a) − β * logπ(a∣s)\]

action-value function: Q(s, a) ≈ E\[r + γ * E\[V(s′)\]\]

loss function critic: J_Q(θC) = \[1/2 * (Q_θC(s, a) − (r + γ * E\[V_θC(s′)\])) ** 2\]

loss function actor: J_π(θA) = E\[β * log(π_θA(a∣s)) − Q_θC(s, a)\]

Gym/SB3

Stable Baselines3 (SB3) es una biblioteca de Python que nos proporciona implementaciones estables y fáciles de usar de algoritmos de aprendizaje por refuerzo. La herramienta tensorboard sirve para visulizar los datos recopilados durante el entrenamiento. gymnasium es otra biblioteca también de Python desarrollada por OpenAI que proporciona una variedad de entornos para aplicar algoritmos de aprendizaje por refuerzo, la usaremos para familiarizarnos con la librería stable_baselines3 y poner en práctica los conocimientos sobre deep RL. Por lo tanto, necesitamos instalar las siguientes librerías:

pip install gymnasium tensorboard stable_baselines3

En esta última librería, existen tres tipos de políticas:

MlpPolicy: trabaja con estados en forma de vectores, por ejemplo, en el entorno de CartPole.
CnnPolicy: los estados son imágenes, como en el juego de Atari.
MultiInputPolicy: las observaciones son de diccionarios para permitir la entrada de diferentes tipos de datos.

Hemos desarrollado un programa en Python para crear y entrenar un modelo diseñado para tres entornos específicos de Gym. El parámetro log interval es un opcional y por defecto es 1. Los resultados pueden visualizarse directamente mediante el comando tensorboard. En algunos casos se pueden normalizar los estados y/o recompensas para que el entrenamiento sea más estable y acelerar su convergencia. Un rollout puede tener una duración fija (número de steps) o varaible (steps llevados a cabo en un episodio), esto depende de como se configure el parámetro train_freq. También hemos creado un script que evalúa el modelo en inferencia y visualiza los resultados, permitiéndonos probar varios modelos a la vez para facilitar la comparación.

python3 train.py --env $ENV --alg $ALG --log_interval $LOG_INTERVAL
tensorboard --logdir=$DIR
python3 train.py --env $ENV --alg $ALG

Hemos utilizado estos juegos como entornos para nuestro programa:

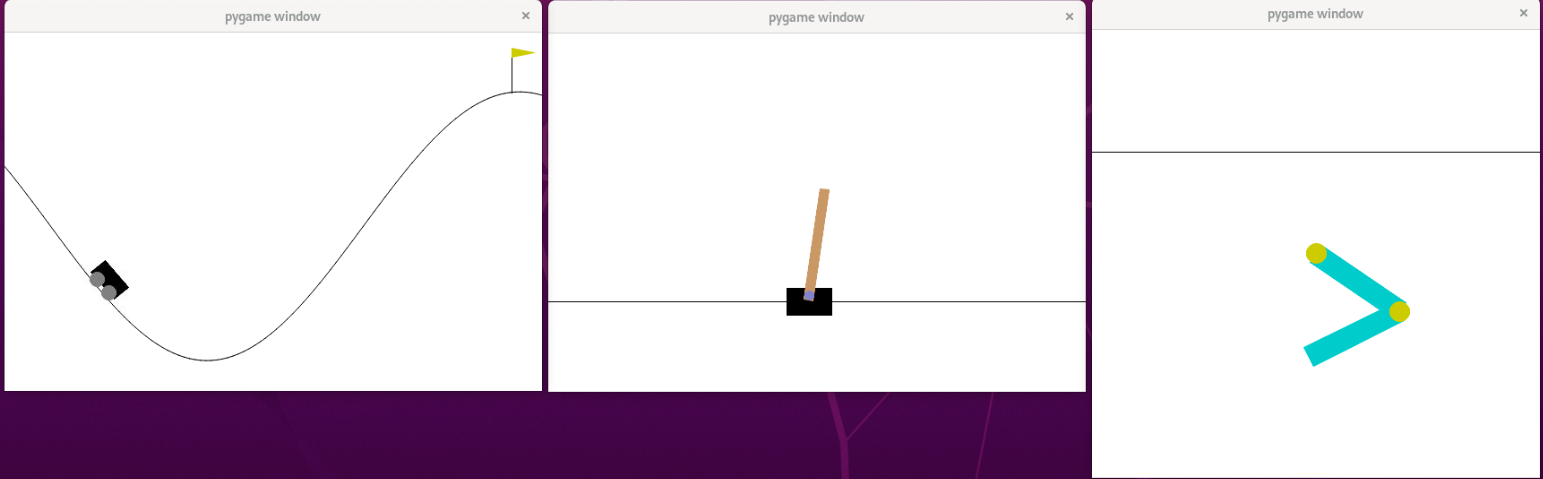
CartPole: consiste un carro que sostiene un poste, cuyo objetivo es mantener el poste dentro de un cierto ángulo tanto tiempo como sea posible, moviéndose hacia la izquierda o hacia la derecha. Recibe una recompensa de +1 en cada paso que el poste permanece dentro del ángulo deseado. Cada estado del juego incluye la posición y velocidad del carro, además del ángulo del poste y la velocidad angular del poste. Un episodio termina si el poste supera el ángulo especificado, si el carro se sale de los límites del juego o se supera una puntuación de 500.
MountainCar: un coche no tiene suficiente potencia para subir una montaña y su objetivo es aprender a utilizar las físicas del entorno para lograr subirlo. El entorno proporciona una recompensa de -1 en cada paso que el coche no alcanza la cima de la montaña. Los estados incluyen la posición y la velocidad del vehículo, y hay tres acciones posibles: acelerar hacia adelante, hacia atrás o no acelerar. Un episodio termina si el coche alcanza la cima de la montaña o si se alcanza un número máximo de pasos. En este juego, cuando se emplean modelos que admiten un espacio de acciones continuo, usamos el entorno MountainCarContinuous, pues, por lo general, conseguiremos un modelo más efiente. En este último entorno, el diseño de penalizaciones y recompensas se diferencia del entorno MountainCar clásico.
Acrobot: el objetivo es balancear un péndulo doble hasta que supere cierta altura, desafiando la gravedad. Un estado se define con cuatro variables: los senos/cosenos de los ángulos de los enlaces del péndulo doble y sus respectivas velocidades angulares. Similar a MountainCar, en cada paso que no se supere la altura del umbral, se recibe una recompensa de -1. Un episodio termina cuando se supera esa altura o cuando se alcanza un número máximo de pasos. Las acciones posibles son aplicar un torque negativo, positivo o nulo.

La varianza es la variabilidad en las recompensas de un episodio a otro. La gráfica de explained_variance en la sección de train representa cuánto de esta variabilidad en las recompensas puede ser explicada por el modelo. Un valor cercano a 1 significa que el modelo puede explicar la mayoría de la variabilidad en las recompensas, esto sugiere que el modelo está aprendiendo efectivamente. Sin embargo, es importante tener en cuenta que siempre habrá cierto grado de azar involucrado. A medida que el modelo comienza a converger, las variaciones en las recompensas serán muy pequeñas pero inexplicables (explained_variance menor o igual a 0).

Análisis de resultados

Primero vamos a comparar en espacios discretos. Como se puede observar en la imagen inferior, en el entorno de CartPole, con el algoritmo DQN no conseguimos que el modelo converja, mientras que con PPO y A2C sí. Además, podemos apreciar que con PPO el entrenamiento converge mucho más rápido que con A2C, lo cual puede deberse a que PPO restringe la diferencia entre políticas. En inferencia, esto se traduce en que DQN no consigue el objetivo de mantener el palo erguido durante 500 pasos seguidos, mientras que los otros dos modelos sí lo logran.

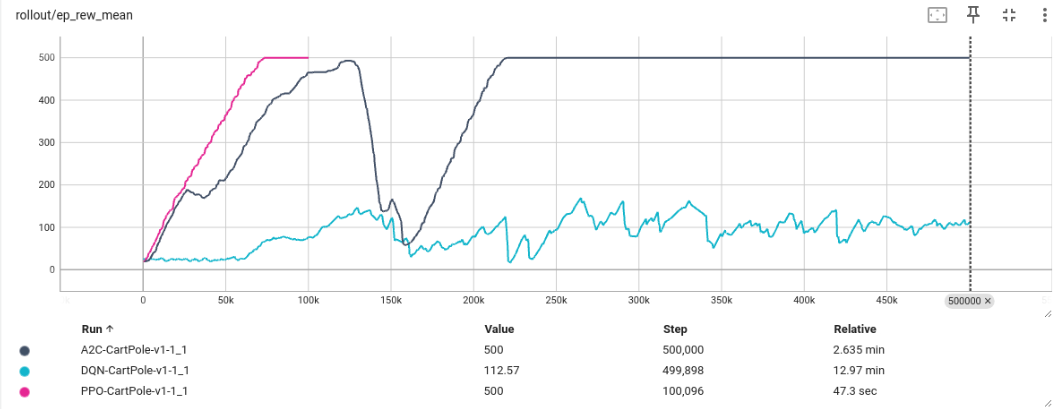
Sin embargo, en el entorno de Acrobot obtenemos mejores resultados con DQN que con A2C o PPO, los cuales producen resultados muy similares. Esto puede deberse a la simplicidad del entorno o la exploración que proporciona DQN. Aunque debemos destacar que en todos los casos los modelos convergen.

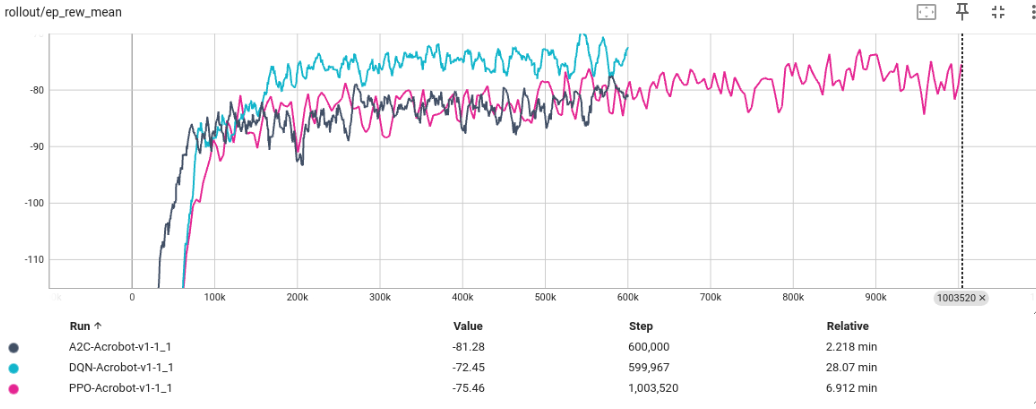
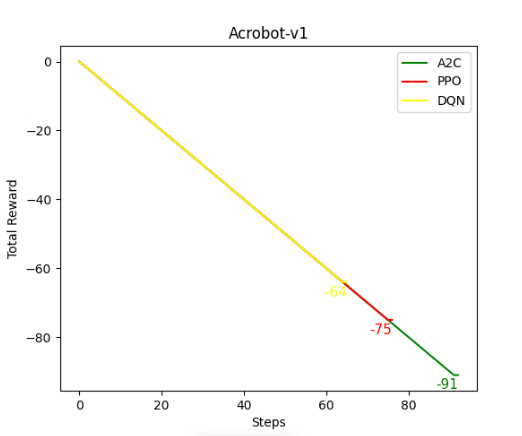
Por otro lado, en el entorno de MountainCar discreto los tres modelos convergen, pero A2C y PPO producen mejores resultados que DQN. Ahora pasamos a evaluar los tres últimos algoritmos, SAC, DDPG y TD3, en la versión continua de MountainCar. En inferencia, vemos que se tarda algunos steps menos en lograr subir la colina en el entorno continuo que en el discreto. Podemos ver que con SAC se consigue antes la convergencia, ya que proporciona una exploración diversa y distintas formas de lograr el objetivo, no es un modelo determinista como en los otros dos casos.

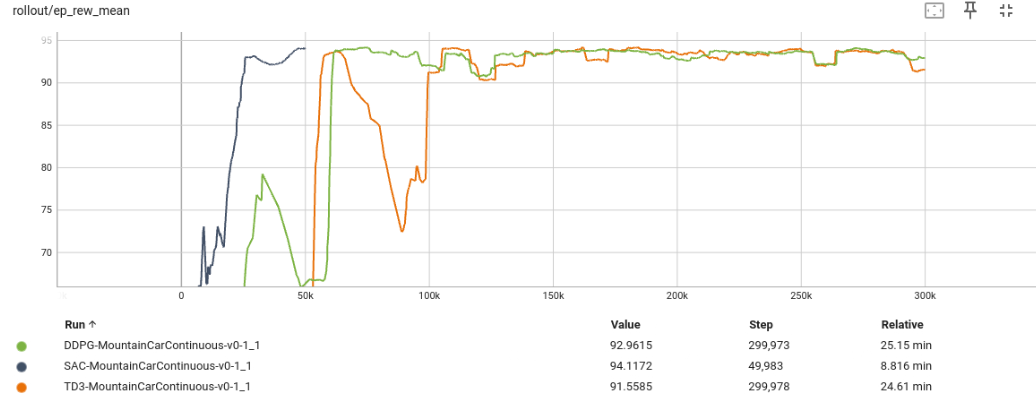
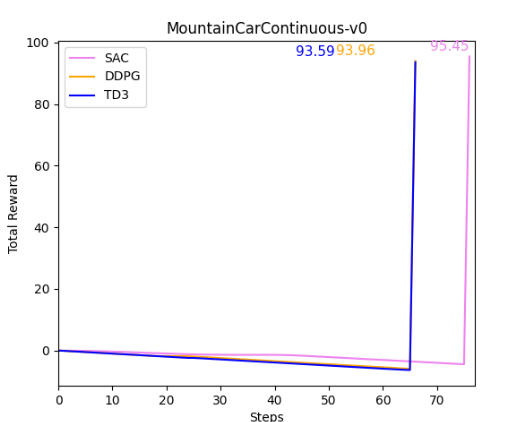
Analizando todos estos datos, nos damos cuenta de que no se puede determinar que un modelo es mejor que otro en sí mismo; depende de la tarea a la que se aplique. Muchas veces es difícil determinarlo a priori que modelo es mejor, y debemos descubrirlo mediante experimentación. Para ver qué modelo elegir para nuestro seguimiento del carril con deep RL, probaremos diferentes modelos en la siguiente sección.

Share on

Twitter Facebook LinkedIn

Lara Poves Martínez