Sigue carril: DRL
Aunque inicialmente comenzamos a realizar los entrenamientos en el antiguo servidor landau, los entrenamientos definitivos se han llevado a cabo en un nuevo servidor exclusivo para nosotros thor. Es importante recordar que, si se desea utilizar pygame, primero se debe ejecutar el siguiente comando en la terminal:
export LD_PRELOAD=/usr/lib/x86_64-linux-gnu/libstdc++.so.6
Índice
Entornos
Para aumentar los frames por segundo y reducir el tiempo de entrenamiento, hemos desactivado la segmentación. Hemos creado tres entornos de Gym que principalmente difieren en la función de recompensa y el espacio de acciones, lo cual determina el tipo de algoritmo que utilizaremos para entrenar. Emplearemos modelos predefinidos de la librería stable-baselines3, como se detalló en el apartado anterior.
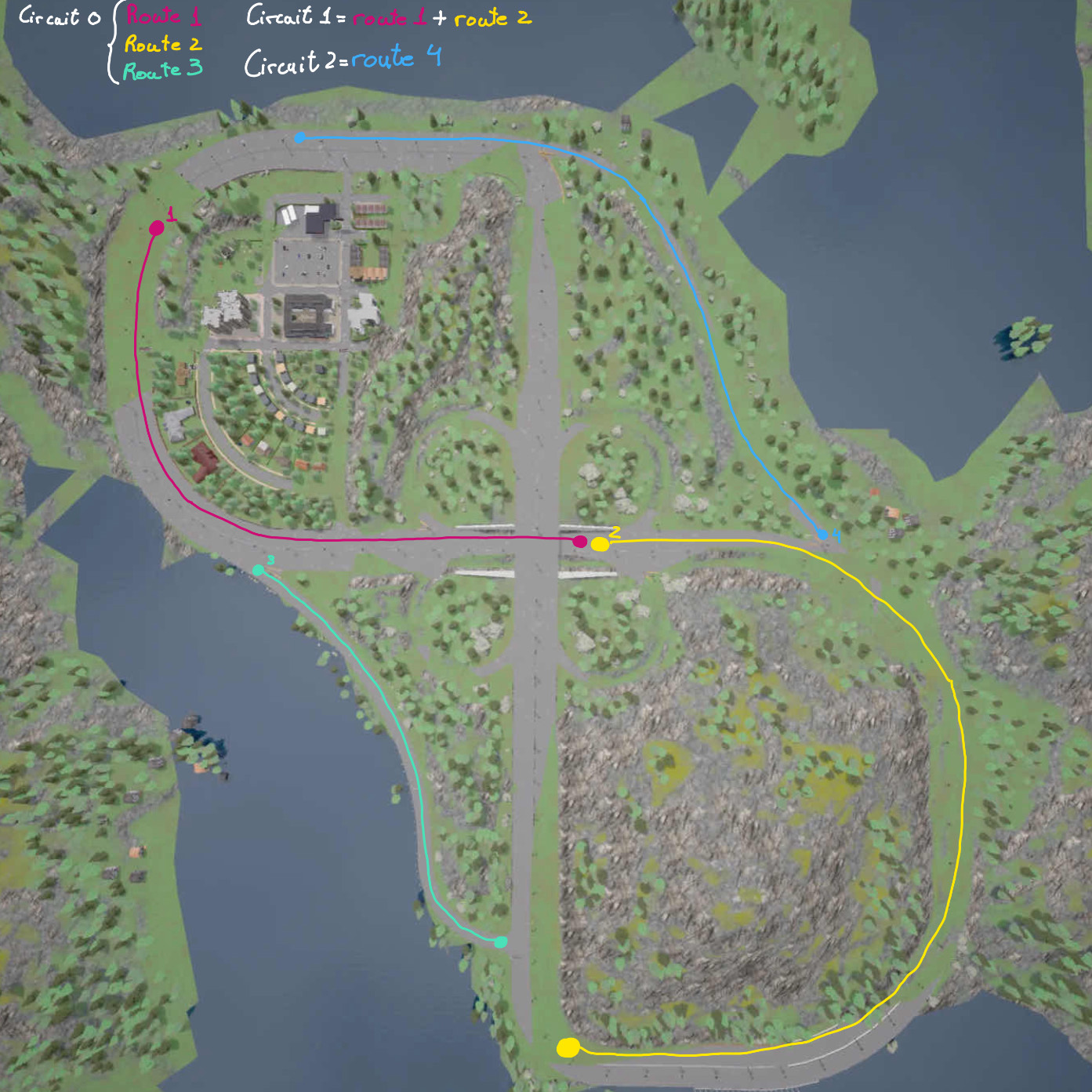
A continuación, se muestra el mapa que define los circuitos disponibles en nuestro entorno en el Town04. El circuito 0 está compuesto por 3 rutas, las cuales utilizamos para entrenar nuestro modelo. La ruta en la que se lleva a cabo cada episodio se elige de manera aleatoria. Cada una de estas rutas comienza en una dirección distinta: curva a la derecha, recto y curva a la izquierda, con el fin de evitar el overfitting del modelo.
Por otro lado, los circuitos 1 y 2 disponen de una sola ruta cada uno. Estos se utilizan para la fase de inferencia para la evaluación del modelo. El circuito 1 corresponde a un recorrido que el modelo ha visto durante el entrenamiento, mientras que el circuito 2 es completamente nuevo, lo que nos permite evaluar el rendimiento del modelo en un escenario desconocido.
El vehículo del entorno consta de los siguientes sensores:
- Sensor de cámara del conductor: detección de carril. Si se pierde la percepción, el episodio se interrumpe (los sensores generan una excepción que se captura).
- Sensor de colisión: si el coche se choca, detenemos el episodio.
- Si está en modo humano: cámara del entorno y activación de pygame.
El espacio de observaciones es continuo y coincide con el espacio de estados. Se normaliza en todos los entrenamientos y está compuesto por múltiples elementos, por lo que utilizamos un espacio de estados basado en un diccionario. Por consiguiente, en nuestros algoritmos emplearemos la política MultiInputPolicy.
- Desviación del carril
- Área del carril
- 5 puntos de la línea izquierda del carril
- 5 puntos de la línea derecha del carril
- Centro de masas
CarlaLaneDiscrete
Este entorno tiene un espacio de acciones discreto, por lo que lo entrenaremos utilizando un algoritmo DQN. Para combinar las acciones de aceleración y giro, hemos seguido la regla de que a mayor aceleración, menor es el giro; aún no se hemos incluido el freno. En total, contamos con 21 acciones disponibles.
self.action_to_control = {
0: (0.5, 0.0),
1: (0.45, 0.01),
2: (0.45, -0.01),
3: (0.4, 0.02),
4: (0.4, -0.02),
5: (0.4, 0.04),
6: (0.4, -0.04),
7: (0.4, 0.06),
8: (0.4, -0.06),
9: (0.4, 0.08),
10: (0.4, -0.08),
11: (0.3, 0.1),
12: (0.3, -0.1),
13: (0.3, 0.12),
14: (0.3, -0.12),
15: (0.2, 0.14),
16: (0.2, -0.14),
17: (0.2, 0.16),
18: (0.2, -0.16),
19: (0.1, 0.18),
20: (0.1, -0.18)
}
Nuestro objetivo es que el coche circule por el centro del carril sin desviarse, manteniendo una conducción fluida y lo más rápida posible. Para lograrlo, hemos diseñado una función de recompensa que se basa principalmente en la desviación del carril y en la velocidad actual del coche, normalizando y ponderando estos valores según sus respectivos pesos. Sin embargo, si el coche pierde el carril o colisiona, el episodio se detiene y se asigna una recompensa negativa.
def _calculate_reward(self, error:str):
if error == None:
# Clip deviation and velocity
r_dev = (MAX_DEV - abs(np.clip(self._dev, -MAX_DEV, MAX_DEV))) / MAX_DEV
r_vel = np.clip(self._velocity, 0.0, self._max_vel) / self._max_vel
reward = 0.8 * r_dev + 0.2 * r_vel
else:
reward = -30
return reward
La pérdida del carril puede deberse a que no se ha detectado una de las líneas, el área es cero o ha habido un cambio de carril, lo que indica que hemos perdido el anterior. Para abordar esta situación, añadiremos una nueva verificación en la función step:
dev_prev = self._dev
self._dev = self._camera.get_deviation()
assert abs(self._dev - dev_prev) <= 5, "Lost lane: changing lane"
Para entrenar, hemos utilizado un fixed_delta_seconds de 50ms, lo que equivale a entrenar a 20 FPS. Por lo tanto, en la fase de inferencia, necesitamos operar al menos a esta velocidad. Los entrenamientos tuvieron una duración de 1 día y un par de horas. Tras realizar diversas pruebas experimentales, identificamos los hiperparámetros que proporcionaron los mejores resultados:
learning_rate: 0.0005
buffer_size: 20_000
batch_size: 1024
learning_starts: 0
gamma: 0.85
target_update_interval: 1024
train_freq: 256
gradient_steps: 2
exploration_fraction: 0.8
exploration_final_eps: 0.0
n_timesteps: 8_000_000
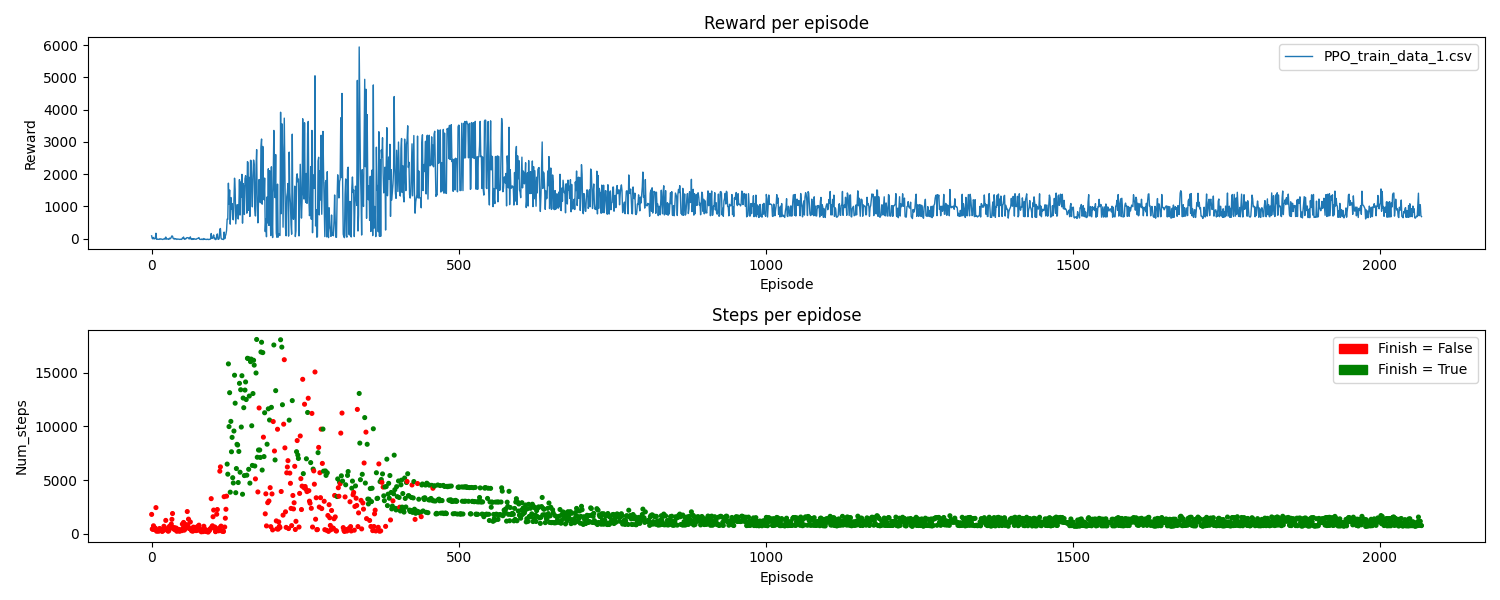
La frecuencia de entrenamiento resultó ser un factor clave en el proceso, al principio se utilizó un valor menor, pero los modelos no lograron converger. El ratio de exploración se reduce gradualmente durante el 80% del entrenamiento y, a partir de ese punto, se dejan de realizar acciones aleatorias (ε=0). En la gráfica siguiente, se puede observar cómo el modelo finalmente converge:
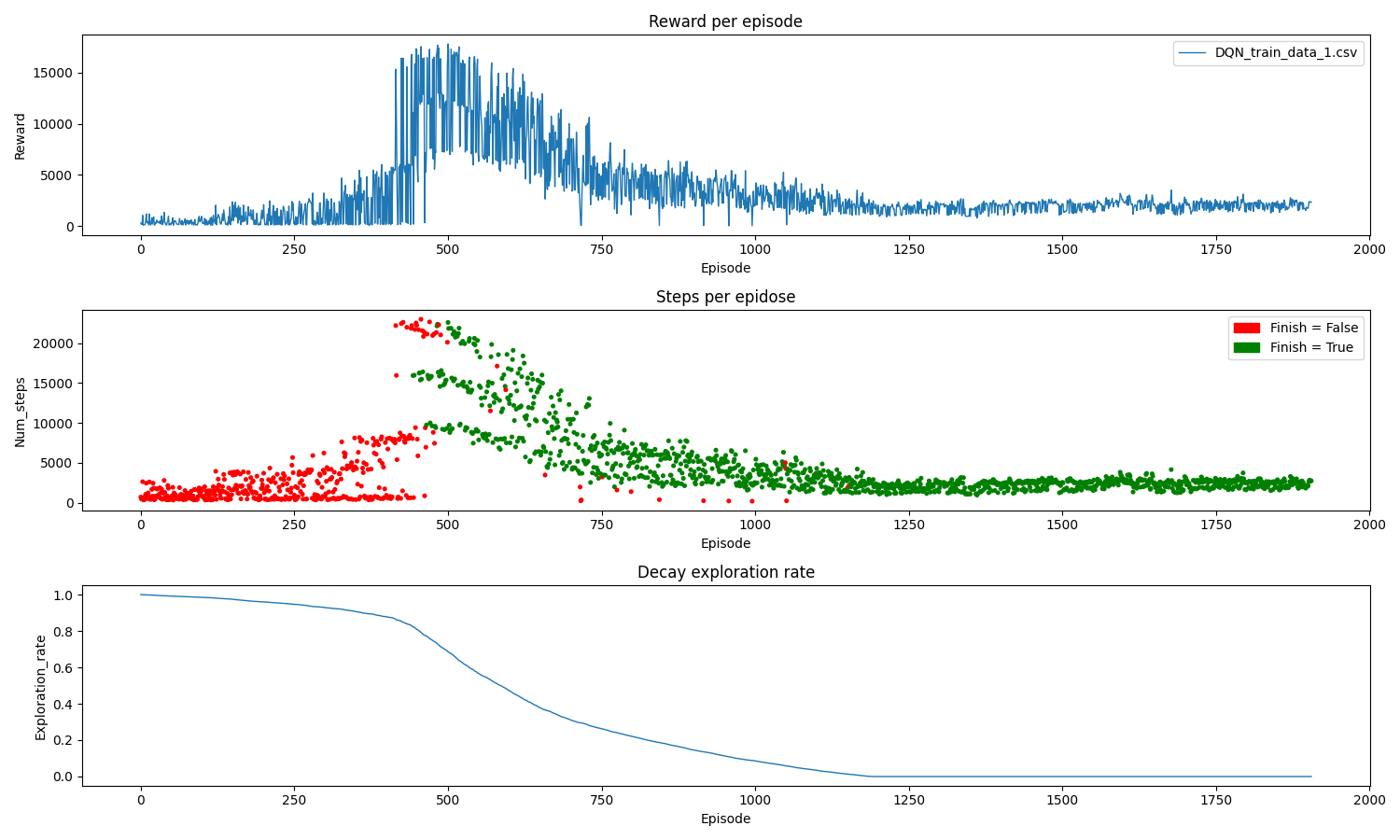
En inferencia en el circuito 1 (visto durante el entrenamiento), se observa que el seguimiento del carril es casi perfecto. No obstante, en algunas ocasiones, cuando el vehículo va en línea recta, se percibe un pequeño balanceo. Esto se debe a una de las limitaciones de DQN, ya que su espacio de acciones es discreto y no permite seleccionar la acción de giro óptima en cada momento. Aun así, un seguimiento del carril completamente perfecto podría ser un indicio de overfitting en nuestro modelo.
En las siguiente gráficas, se presenta la información recopilada durante la inferencia: la aceleración comandada al coche y su velocidad actual, la desviación del carril y la recompensa obtenida, junto con histogramas que muestran las acciones de giro y aceleración escogidas. Podemos observar claramente los momentos en los que se reduce la velocidad, correspondientes a las dos curvas pronunciadas. Sin embargo, de manera general, los histogramas indican que, predominantemente, se eligen los pares de acciones más rápidos.
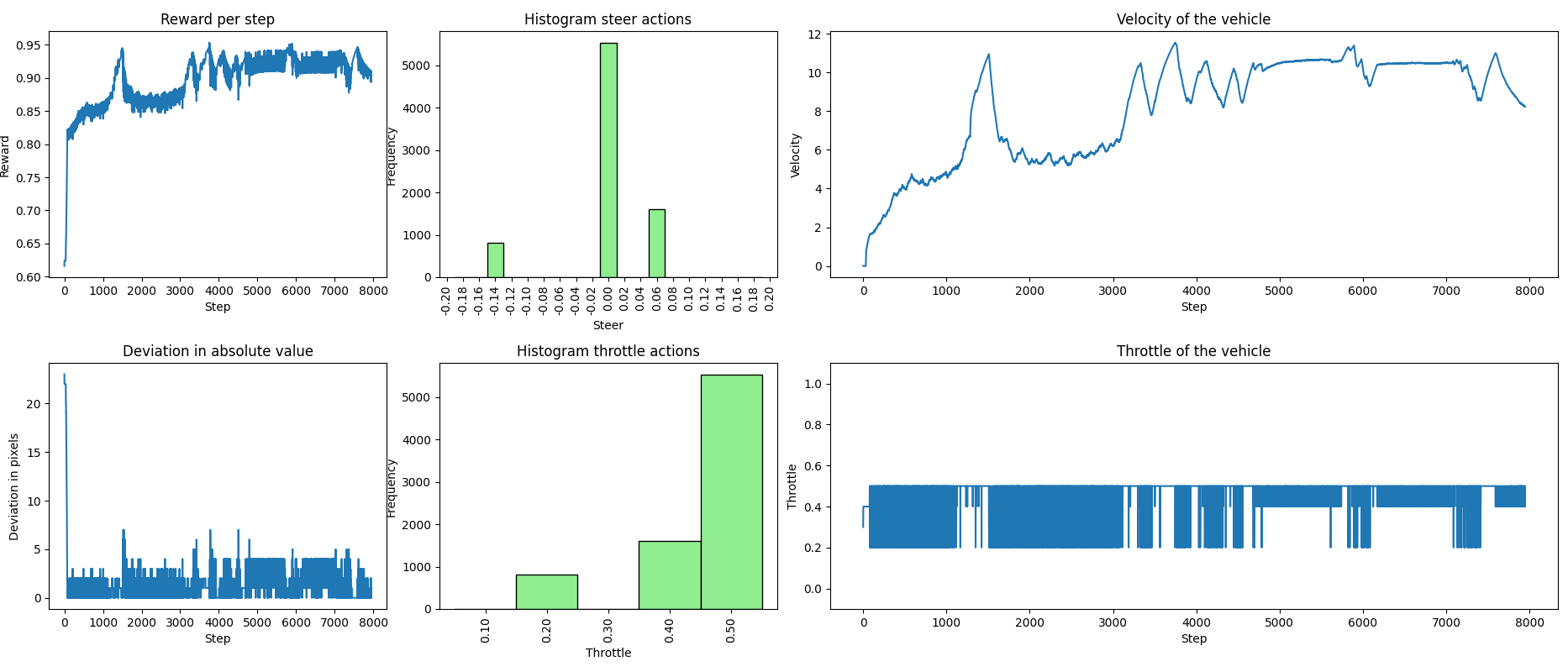
CarlaLaneContinuous
Como hemos comprobado con DQN, el espacio de acciones está restringido. Para conseguir un mejor comportamiento y mayor velocidad, debemos utilizar un algoritmo que permita un espacio de acciones continuo, como PPO. Seguiremos controlando dos elementos: el acelerador y el giro. Permitimos el rango completo para el acelerador (0-1) y limitamos el rango del giro a (-0.2, 0.2):
self._max_steer = 0.2
self.action_space = spaces.Box(
low=np.array([0.0, -self._max_steer]),
high=np.array([1.0, self._max_steer]),
shape=(2,),
dtype=np.float64
)
Para los entrenamientos seguimos utilizando un fixed delta de 50ms (20 FPS), pero hemos introducido cambios en las observaciones:
- Hemos añadido la velocidad actual del vehículo al espacio de observaciones para que pueda entender mejor la función recompensa.
- En lugar de 5 puntos de cada línea del carril, ahora son 10.

La función recompensa sigue el siguiente esquema:
-
Comprobación de errores
Primero se verifica si ha ocurrido un error, como pérdida del carril o choque contra elementos de la carretera. Si ocurre, se finaliza el episodio y se asigna una recompensa negativa. - Normalización lineal de elementos
Si no hay errores, se normalizan los elementos de los que depende la recompensa:- Desviación:
- Se limita el valor de la desviación al rango [-100, 100].
- Se normaliza inversamente, donde una desviación de 0 tiene la mayor recompensa.
- Giro: - Para giros bruscos, la recompensa es nula.
- Para giros no bruscos, se normaliza inversamente considerando el rango [-0.14, 0.14], menores giros mayor recompensa.
- Acelerador: - Si las aceleraciones son bruscas [0.6, 1.0], la recompensa es nula.
- Para aceleraciones no bruscas [0.0, 0.6):
- Si se supera la velocidad máxima, se normaliza inversamente (aceleración 0 tiene mayor recompensa).
- En caso contrario, se normaliza de forma que mayores aceleraciones otorgan mayor recompensa.
- Asignación de pesos a los elementos
Finalmente, se define el peso de cada elemento en la recompensa según los siguientes criterios:- Si el giro o el acelerador son bruscos, tienen un peso muy elevado en la recompensa, mientras que los otros dos elementos tienen un peso mucho menor.
- Si se supera la velocidad máxima, el acelerador tiene mayor peso para intentar frenar, penalizando también el giro debido a la alta velocidad.
- Si el acelerador es bajo [0.0, 0.5), se penalizan menos los giros grandes, facilitando las curvas al reducir la velocidad.
- Si el acelerador está en un rango alto [0.5, 0.6), se penalizan más los giros bruscos, enfocándose en zonas rectas o con giros leves.
if error == None:
# Deviation normalization
r_dev = (MAX_DEV - abs(np.clip(self._dev, -MAX_DEV, MAX_DEV))) / MAX_DEV
# Steer conversion
limit_steer = 0.14
if abs(self._steer) > limit_steer:
r_steer = 0
else:
r_steer = (limit_steer - abs(self._steer)) / limit_steer
# Throttle conversion
limit_throttle = 0.6
if self._throttle >= limit_throttle:
r_throttle = 0
elif self._velocity > self._max_vel:
r_throttle = (limit_throttle - self._throttle) / limit_throttle
else:
r_throttle = self._throttle / limit_throttle
# Set weights
if r_steer == 0:
w_dev = 0.1
w_throttle = 0.1
w_steer = 0.8
elif r_throttle == 0:
w_dev = 0.1
w_throttle = 0.8
w_steer = 0.1
elif self._velocity > self._max_vel:
w_dev = 0.1
w_throttle = 0.65
w_steer = 0.25
elif self._throttle < 0.5:
w_dev = 0.65
w_throttle = 0.25
w_steer = 0.1 # Lower accelerations, penalize large turns less
else: # [0.5, 0.6) throttle
w_dev = 0.6
w_throttle = 0.15
w_steer = 0.25
reward = w_dev * r_dev + w_throttle * r_throttle + w_steer * r_steer
else:
reward = -40
return reward
Desarrollamos un programa para analizar la exploración de acciones durante el entrenamiento, cuyos resultados se presentan en el siguiente histograma.
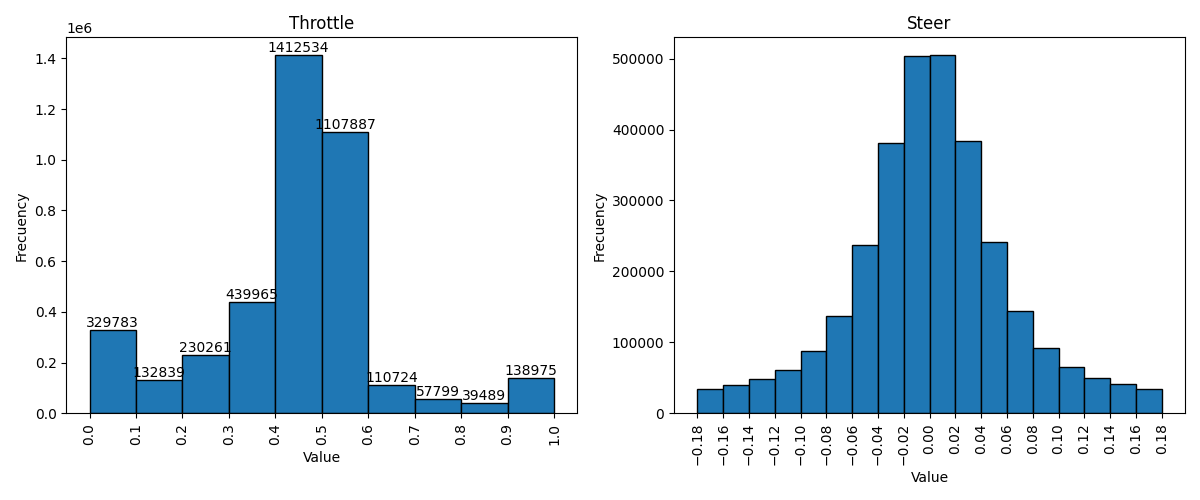
Parémetros de entrenamiento
Al igual que en el entrenamiento anterior, el parámetro n_steps fue clave. Además, el batch_size también tuvo un gran impacto: inicialmente, con valores bajos no lograba converger. Por último, el coeficiente de entropía fue fundamental, ya que con valores bajos siempre aprendía las acciones límite y con valores altos no llegaba a converger.
policy: "MultiInputPolicy"
learning_rate: 0.0001
gamma: 0.85
gae_lambda: 0.9
n_steps: 512 # The number of steps to run for each environment per update
batch_size: 512
ent_coef: 0.1 # β
clip_range: 0.15
n_timesteps: 4_000_000
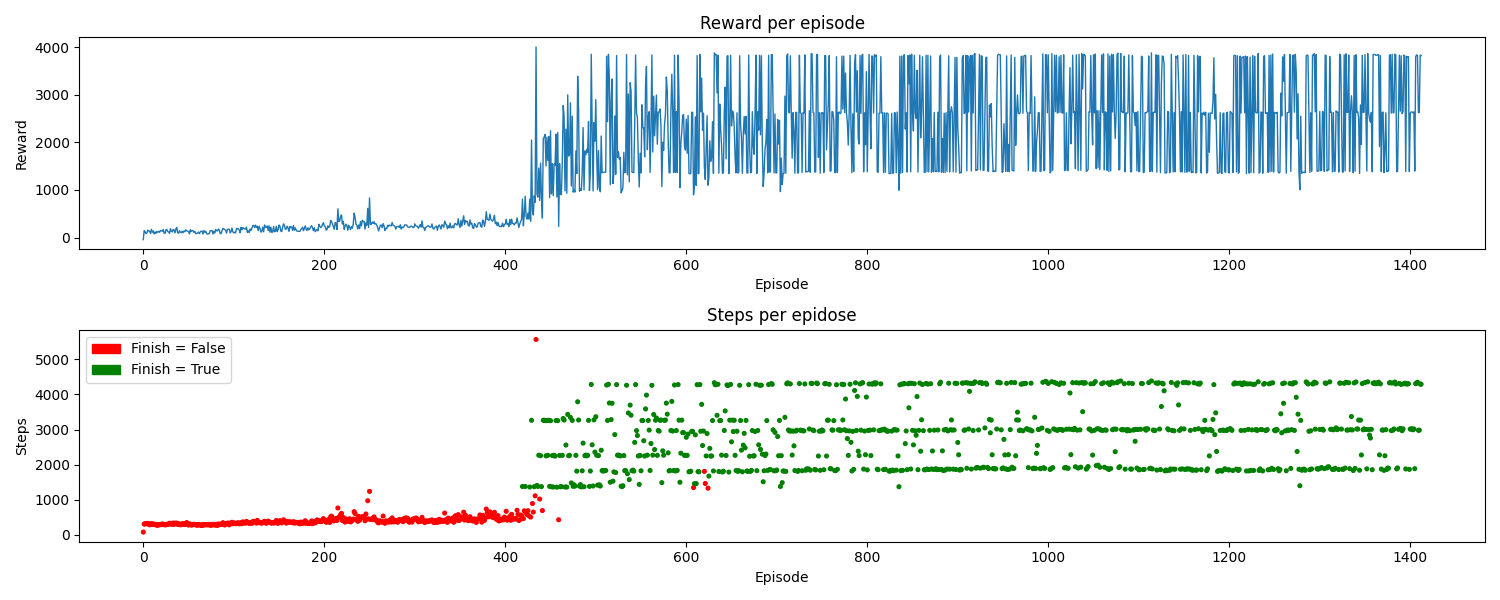
Vemos cómo finalmente el entrenamiento converge con pocos episodios y de forma óptima.
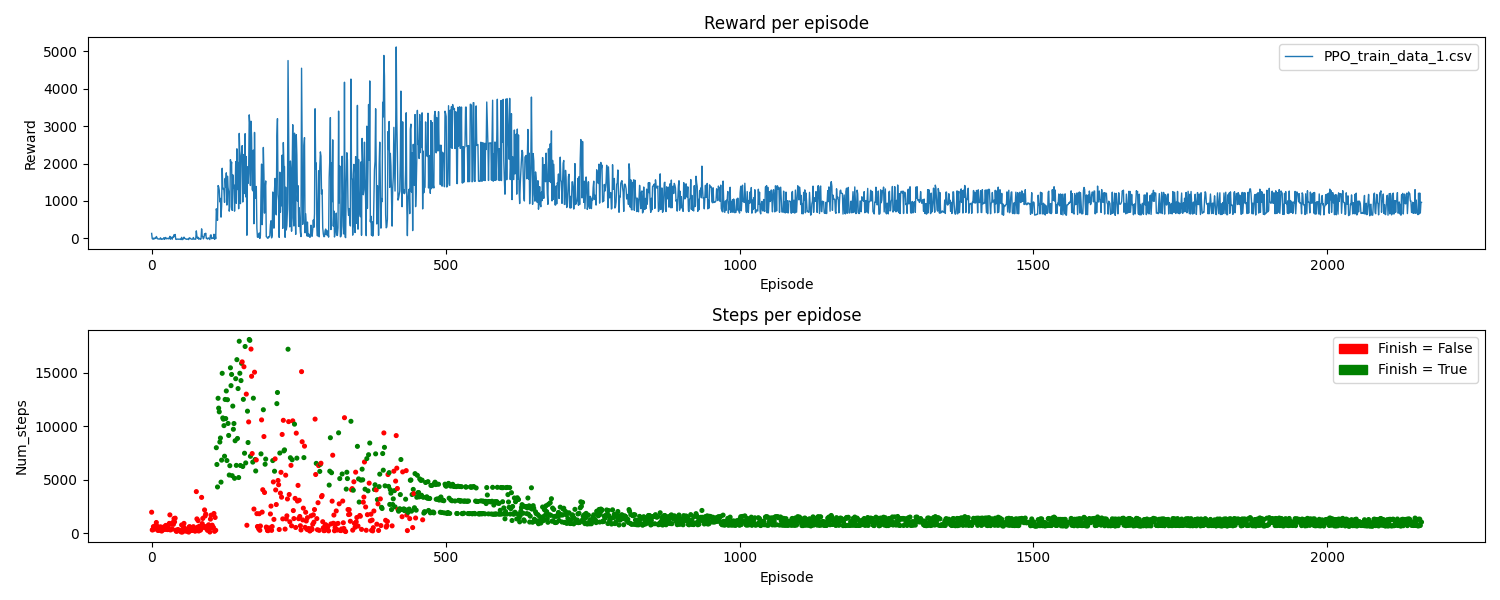
En inferencia obtenemos muy buenos resultados, alcanzando grandes velocidades, superiores a 20 m/s. Finalmente, el modelo elige aceleraciones solo en el rango [0.5, 0.6) combinadas con giros sutiles. De este modo, se consigue seguir el carril de forma óptima y con una conducción suave. Cabe destacar que, si eliminamos la parte del rango bajo del acelerador ([0.0, 0.5)) en la función recompensa, unificando ambos rangos en uno con los mismos pesos, el entrenamiento no logra converger, aunque al final siempre seleccione el último rango.
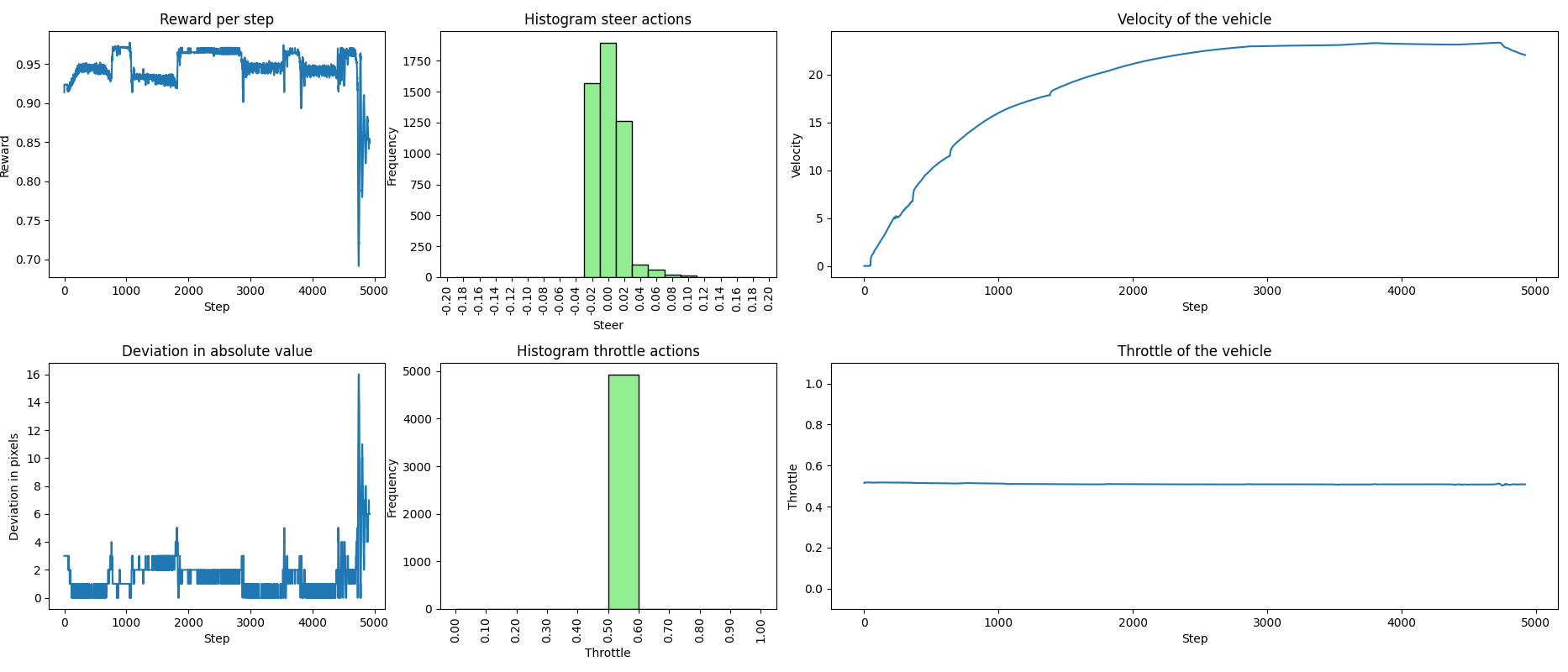
Este es el resultado del entrenamiento en un circuito visto durante el entrenamiento:
También hemos llevado a cabo pruebas en inferencia en varios circuitos que no se utilizaron durante el entrenamiento (como el circuito 2) y en otros de diferentes ciudades (Town03 y Town06). Estos son los resultados obtenidos:
Hemos evaluado si el modelo entrenado utilizando la percepción del carril basada en ground truth funcionaría con una configuración diferente de la cámara y empleando percepción mediante una red neuronal. Los resultados obtenidos han sido satisfactorios.
CarlaObstacle
En este entorno, el objetivo es que el coche siga el carril mientras mantiene una velocidad de crucero definida por otro vehículo que circula delante a una velocidad constante durante todo el episodio. Durante el entrenamiento, esta velocidad se ha fijado a de 7m/s.
Hemos añadido a las observaciones 20 puntos correspondientes a la zona frontal del láser, que en publicaciones anteriores identificamos como la región FRONT. Si el láser no proporciona suficientes mediciones, estos puntos se rellenan con su rango máximo, establecido en 19.5 metros, ya que más allá de esta distancia las mediciones son menos precisas y de menor calidad. En caso de haber más puntos de los necesarios, se seleccionan de forma uniforme, asegurando una distribución equidistante y respetando el orden basado en la coordenada x. A continuación, se presentan ejemplos ilustrativos de estas configuraciones:
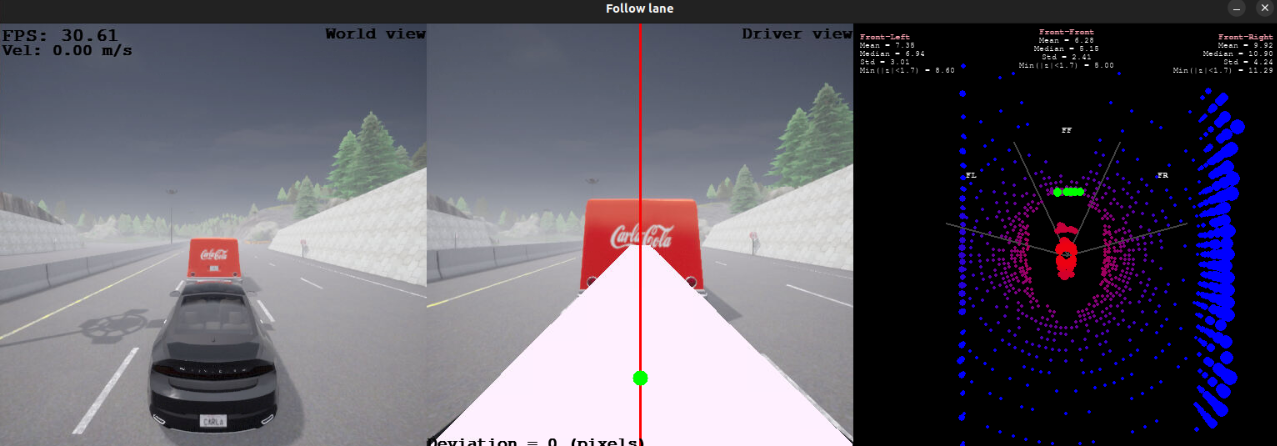
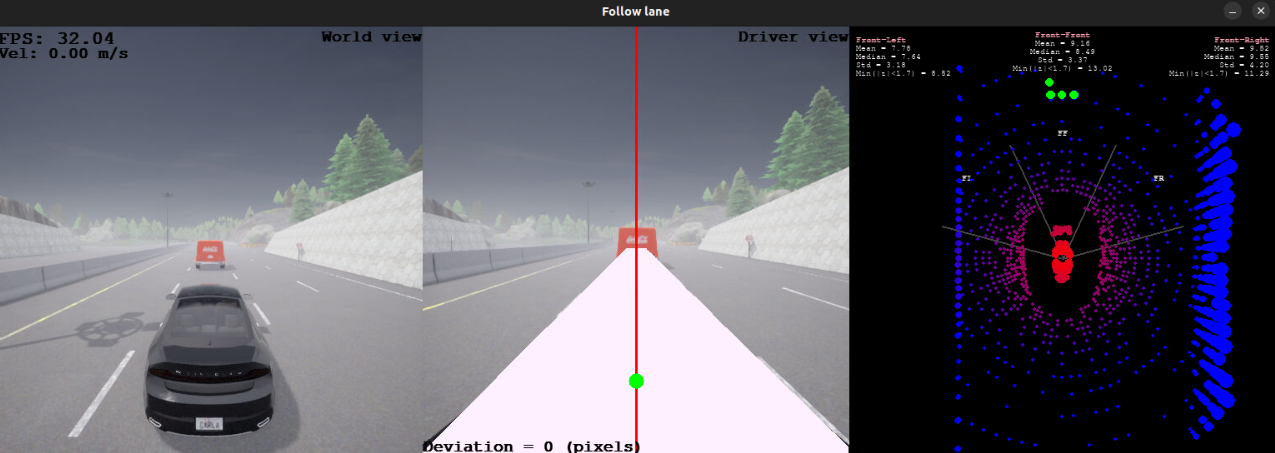
Para este entorno, inicialmente entrenamos un modelo capaz de seguir el carril, reutilizando los parámetros de entrenamiento óptimos previamente determinados. Basándonos en la función de recompensa utilizada anteriormente, normalizamos todas las medidas y calculamos la recompensa final asignando diferentes pesos a los valores involucrados. Cuando no hay mediciones del láser, los pesos son muy similares a los de la función de recompensa original. Sin embargo, al incorporar nuevas observaciones, fue necesario realizar pequeños ajustes para obtener el comportamiento deseado. En estos casos, el peso del láser se establece en 0.
Para lograr el comportamiento deseado, el modelo debe ajustar su velocidad en función del vehículo que tiene delante, evitando colisiones en todo momento. Si el coche se aproxima demasiado al vehículo delantero (menos de 4 metros), se considera una colisión, lo que resulta en la finalización del episodio con una penalización muy severa (-60). Esta penalización es mayor que la de salirse del carril (-40), ya que una colisión se considera una acción más crítica.
Para este propósito, utilizamos el modelo anterior y lo reentrenamos modificando únicamente la parte de la función de recompensa relacionada con las mediciones del láser. Los mismos parámetros de entrenamiento fueron reutilizados, con la excepción del número total de pasos, que en este caso se redujo a 3_000_000 para optimizar el tiempo de entrenamiento.
Cuando tenemos mediciones del láser, el peso asignado al láser y el de los demás parámetros se ajustan según la distancia al vehículo que se encuentra delante. Es importante destacar que si la distancia es menor de 8 metros, el throttle se recompensa de forma inversa: a menor throttle, mayor recompensa. Por el contrario, si la distancia es mayor a 8 metros, se recompensa de manera directa: a mayor throttle, mayor recompensa.
if error == None:
# Deviation normalization
r_dev = (MAX_DEV - abs(np.clip(self._dev, -MAX_DEV, MAX_DEV))) / MAX_DEV
# Steer conversion
limit_steer = 0.14
if abs(self._steer) > limit_steer:
r_steer = 0
else:
r_steer = (limit_steer - abs(self._steer)) / limit_steer
# Throttle conversion
limit_throttle = 0.6
if self._throttle >= limit_throttle:
r_throttle = 0
elif self._velocity > self._max_vel:
r_throttle = (limit_throttle - self._throttle) / limit_throttle
else:
r_throttle = self._throttle / limit_throttle
# Laser conversion
laser_threshold = 8
if self._is_passing_ep and not np.isnan(self._dist_laser):
r_laser = np.clip(self._dist_laser, MIN_DIST_LASER, MAX_DIST_LASER) - MIN_DIST_LASER
r_laser /= (MAX_DIST_LASER - MIN_DIST_LASER)
if self._dist_laser <= laser_threshold:
r_throttle = (limit_throttle - self._throttle) / limit_throttle
else:
r_laser = 0
# Set weights
if r_steer == 0:
w_dev = 0.1
w_throttle = 0.1
w_steer = 0.8
w_laser = 0
elif r_throttle == 0:
w_dev = 0.1
w_throttle = 0.8
w_steer = 0.1
w_laser = 0
elif self._velocity > self._max_vel:
w_dev = 0.1
w_throttle = 0.65
w_steer = 0.25
w_laser = 0
elif r_laser != 0:
if self._dist_laser <= laser_threshold: # Short distance (4, 8]
w_dev = 0.2
w_throttle = 0.1 # brake
w_steer = 0
w_laser = 0.7
elif self._dist_laser <= 12: # Medium distance (8, 12]
w_dev = 0.45
w_throttle = 0.0
w_steer = 0.05
w_laser = 0.5
else: # Large distance (12, 19.5]
w_dev = 0.45
w_throttle = 0.1
w_laser = 0.35
w_steer = 0.1
w_steer = 0.1
elif self._throttle < 0.5:
w_dev = 0.65
w_throttle = 0.25
w_steer = 0.1 # Lower accelerations, penalize large turns less
w_laser = 0
else: # [0.5, 0.6) throttle
w_dev = 0.6
w_throttle = 0.15
w_steer = 0.25
w_laser = 0
reward = w_dev * r_dev + w_throttle * r_throttle + w_steer * r_steer + r_laser * w_laser
else:
if "Distance" in error:
reward = -60
else:
reward = -40
return reward
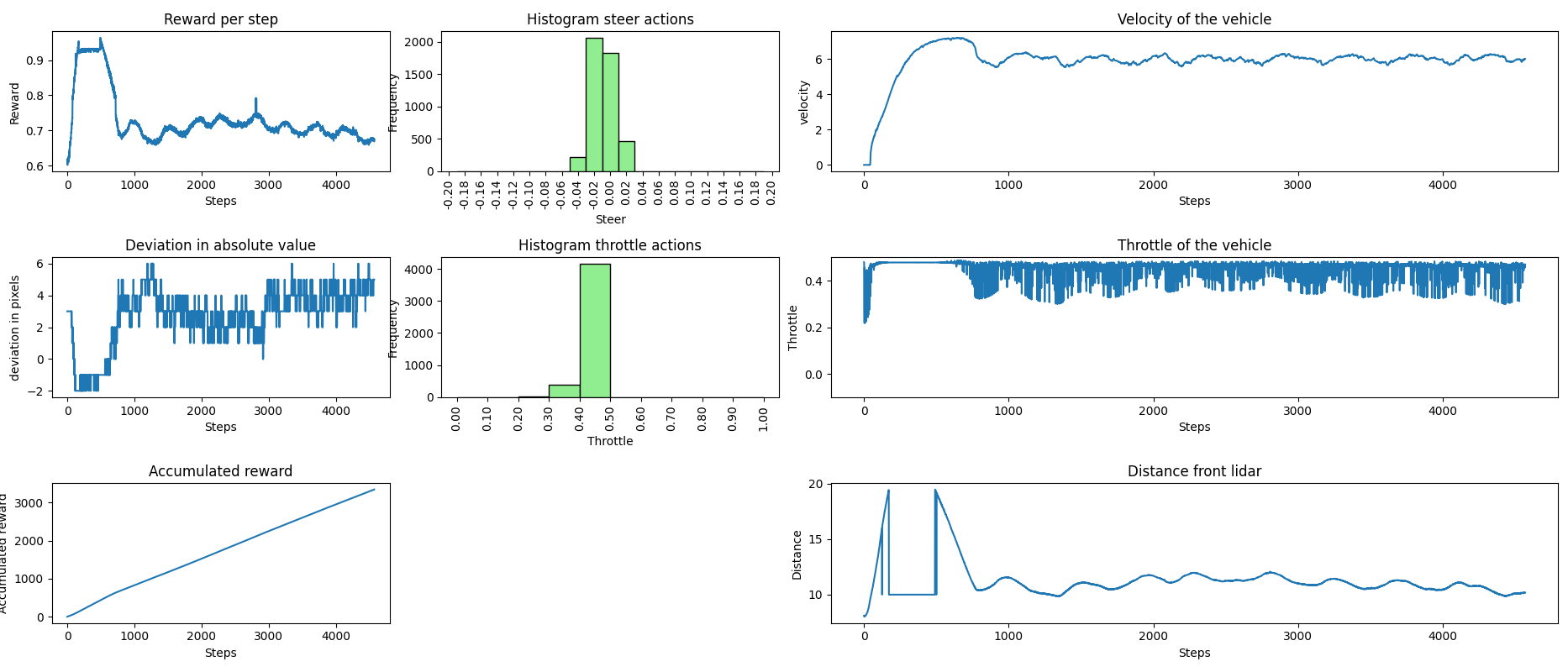
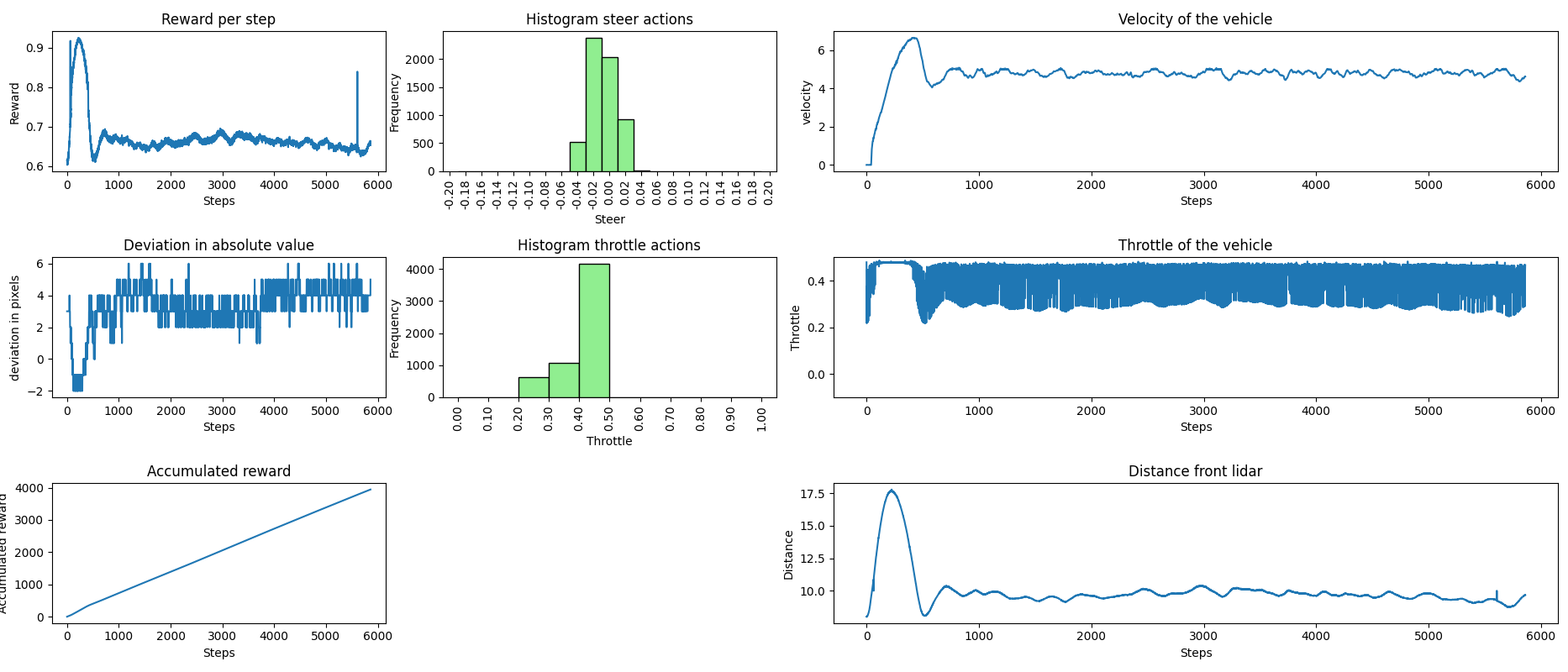
Finalmente, logramos que nuestro vehículo mantuviera, con cierta estabilidad, la velocidad de crucero establecida por el vehículo delantero durante todo el recorrido, asegurando que no ocurrieran colisiones. A continuación, se presentan los datos recopilados durante la fase de inferencia. En la primera imagen, el vehículo delantero mantuvo una velocidad constante de 6.2 m/s, mientras que en la segunda imagen circulaba a 5 m/s.
Estos son los videos que ilustran los comportamientos descritos en las gráficas anteriores.
CarlaPassing
obs añadidas -> contar que haora entrenamos a 10 FPS
entrenamientos base
lane params: PPO: policy: “MultiInputPolicy” learning_rate: 0.0001 gamma: 0.85 gae_lambda: 0.9 # γ n_steps: 512 # The number of steps to run for each environment per update batch_size: 512 ent_coef: 0.08 clip_range: 0.15 # epsilon n_timesteps: 4_000_000
hemos bajado el ent coef ya queafecta a la aleatoriedad en elegir acciones, y dificualtaba la convergencia del entrenameinto al final
-
func recompensa, podemos quiatr el elif qu ehabia en los anteriores entornos, sin elllos en los anteriores no funcionaba. Tambien es el entrnamiento que nos ha proporcionado mayores velocidades. Con al func de recompensa antrior se quedba atascdo en 12m/s, aun qu eaumentasemos el peso del acelerador solo se conseguia un maximo de 18m/s y se quedaba tascado ahi
-
vidoe lane
-
explicar lser
-
video laser
hemos eliminado la 3 al entrenar el adelantamiento (no el seguimiento del carril, ni el no chocarse) porque detectamos la vaya lateral con el lidar, lo que nos impde saber si hemos adelantado completamente al coche o es la vaya.
maquina de estados
func recompensa + maquina de estados
resultados
