Robot following path to goal with q learning and sarsa
Reqs
To execute this program you just need to install the following libraries:
- Python3
- PyQt5
- numpy
- Pandas
- matplotlib
Manual
The main goal of this kind of exercises is to learn how to develop a simple reinforced learning algorithm to make an agent learn the optimal path to the goal as soon as possible. The provided environment gives the possibility to perform one of four actions (“go up”, “go down”, “go left” and “go right”) each simulation step to try getting closer to the location/state in the board which was configured as goal.
GRAPHS:
To learn the behaviour of our agent based on what we are implementing it is important to have any kind of metric to measure the performance of each test. To accomplish that we have two graphs in the upper part of a window that will be prompted each time the agent complete a configured number of maximum attempts to reach the goal.
-
The first graph indicates how good the agent is learning a path so the total reward is for each run increases. This graph shows the total reward per run.
-
The second graph indicates how many steps were needed in each run to either reach the goal or fail (getting out of the board or stepping a bomb)
BOARD:
Nevertheless, to ease the analysis of each try, it is always a good idea to represent the real scenario as clos to reality as possible. For that reason, a board is represented in the down side of the window with the number of times our agent steps each cell of the board before finishing the run. To better have an idea of the final learning of our agent we will display the most recurrents paths followed and the number of occurrences of those paths.
CONFIGURATION
Instead of not being really configurable, the code is easily modifiable to try different scenarios and to visualize more or less number of occurrences. In order to do so, comments and constants with descriptive names have been added at the beginning of the code. Nevertheless, the main constants that take part in this configuration are described below:
To configure the environment open the environment.py file and adjust the following parameters according to your needs:
- NUM_OF_X_BLOCKS: Number of the board blocks in x axis
- NUM_OF_Y_BLOCKS: Number of the board blocks in y axis
- INIT_Y: Initial position that the robot will occupy in the board y axis
- INIT_X: Initial position that the robot will occupy in the board x axis
- BLOCKS: list containing the meaning of each cell in the board (“GOAL”, “BOMB”, “OK”)
To configure the algorithm that will be used to solve the problem adjust the following hyperparameters in robot_mesh.py file:
- GAMMA
- LEARNING RATE
- EXPLORATION_MIN
- EXPLORATION_DECAY
And finally, to visualize the desired number of last occurrences, configure the constant “NUMBER_OF_LAST_OCCURRENCES_TO_PLOT” in robot_mesh.py (E.g If configured to 10, then the last 10 occurrences will be shown in the “results window” displayed at the end of the program execution)
Videos
Code
Path learning to reach a goal using qlearning
Results
The easiest and fastest way to solve this problem was proved to be q learning. After some hyperparameters tunnings to improve the performance and some differents maps tested, the chosen map to exemplify the problem results is the following:

Being the green cells the start and end points, the black cells the bombs that the “robot” must avoid and the blue cells the optimal path to achieve the goal. The winners hyperparameters have been the following:
- GAMMA = 0.95
- LEARNING RATE = 0.9
- EXPLORATION_MIN = 0.000001
- EXPLORATION_DECAY = 0.999
And the results, as shown in the video are indicated within the following graphics:
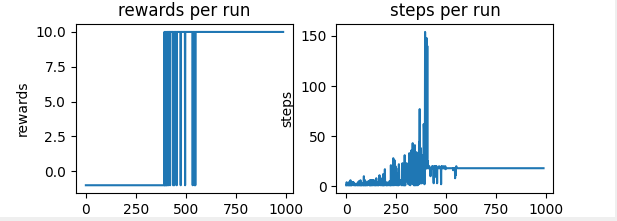
As you can see, the algorithm converges around the simulation 450, from which all the paths followed were the optimal.
After this experiment I felt it was not enough and Sarsa was implemented to solve the same problem. Note that Sarsa tries to converge with as less risk as possible, avoiding paths close to a low reward. For that reason, the map shown in the q learning example never converged using Sarsa. Once the map was a little more clear with wider paths to the goal, Sarsa got to learn a path to the goal even not being the optimal one. You can find the explanation of this in the best answer to this question.
that said, having this map:
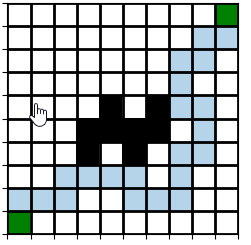
And the following chosen hyperparameters:
- GAMMA = 0.9
- LEARNING RATE = 0.9
- EXPLORATION_MIN = 0.001
- EXPLORATION_DECAY = 0.9995
Those are the (obvously worse) results:
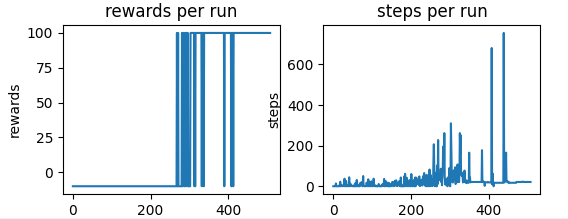
Feel free to share a better implementation or discrepancies with our conclussions!! We are humbly open to learn more from more experts!!