Previous weeks - First trainings
Training Non-Recurrent Neural Networks
The first step was to try to solve the problem of prediction with a classical neural network that does not use recurrence. We carry out the training of different networks with the generated data.
Linear Functions dataset
The first thing we must do to train the network for prediction is to resize the data to ensure that the input shape is correct. For the function data we must have the following shapes:
input_shape=(n_samples, know_points=20, 1)
output_shape = 1
For this type of data we have trained a simple MLP whose structure can be seen in the following figure:
As you can see in the following image, the network manages to reduce and stabilize the loss function in only a few epochs, obtaining a very reduced error.
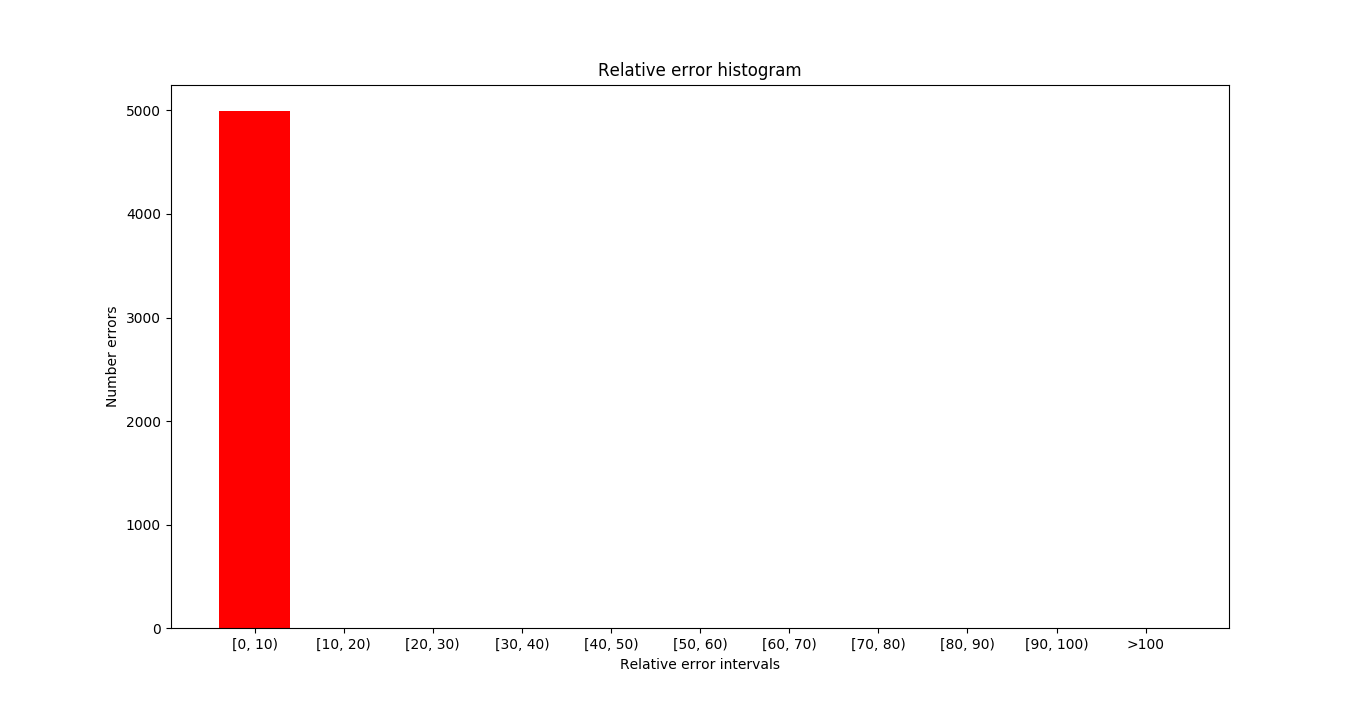
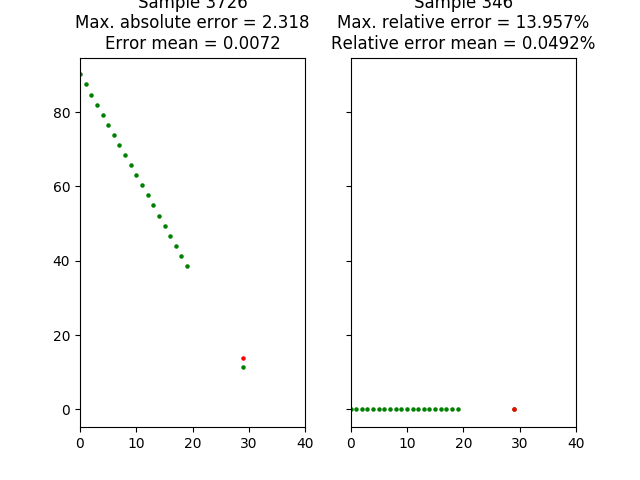
In the next image you can see the samples where the errors (absolute and relative) are maximum. In the case of relative error, when the line has a small slope the relative error is very high, this is because we divide by a very small value.
URM Vectors dataset
As in the functions case, the first thing we must do to train the network for prediction is to resize the data to ensure that the input shape is correct.In this case we must have the following shapes:
input_shape=(n_samples, know_points=20, vector_length=320)
output_shape = vector_length
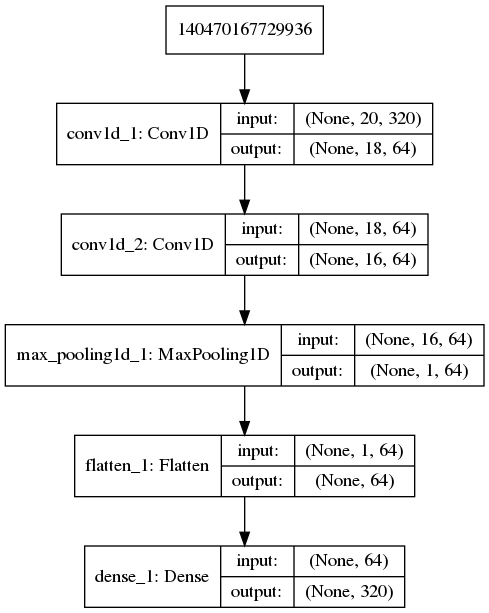
For this type of data we have trained 1D convolutional network whose structure can be seen in the following figure:
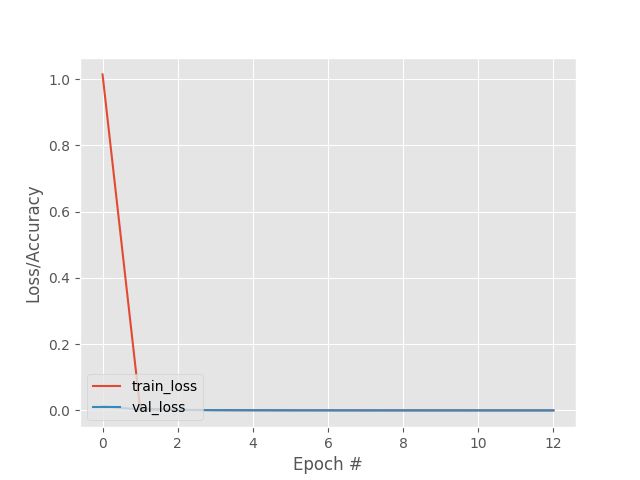
As expected and as it happened in the non-recurring case, the network manages to reduce and stabilize the loss function in only a few epochs, without any error.
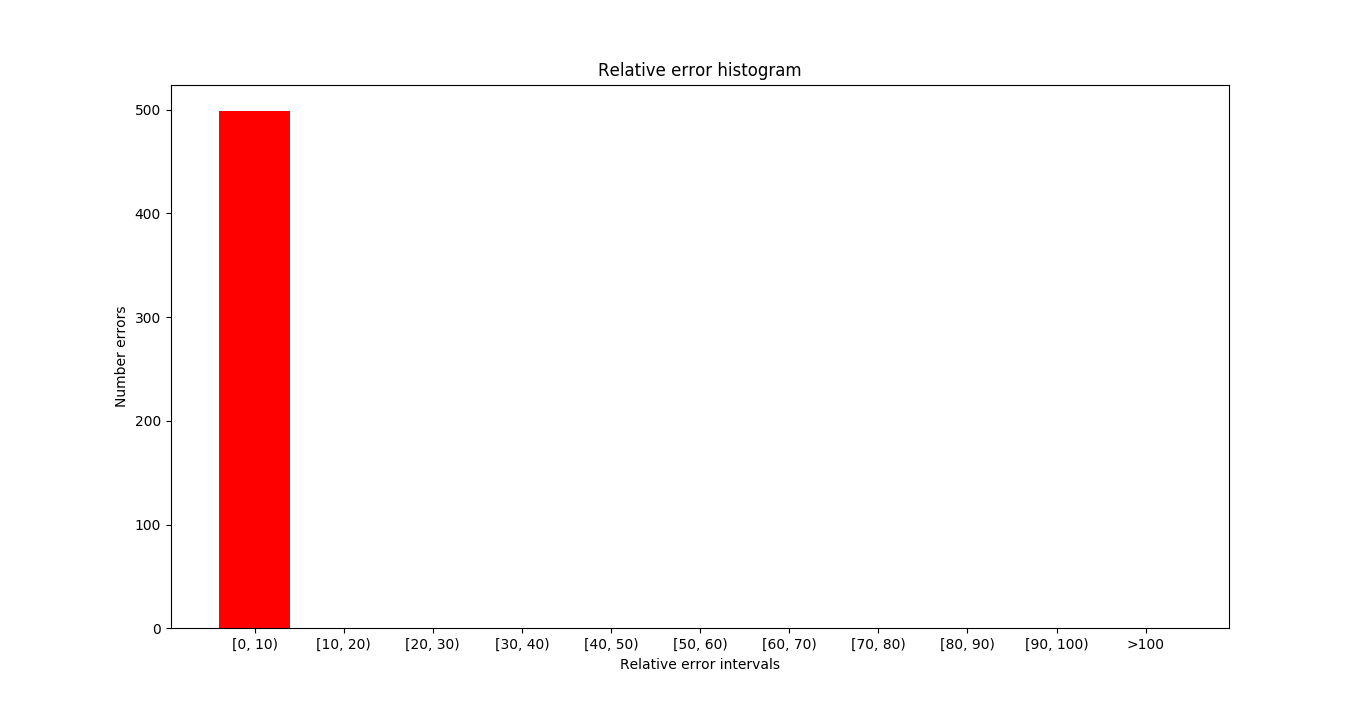
In the next image you can see the samples where the errors (absolute and relative) are maximum. In this case we have not obtained any error so the first sample is shown.
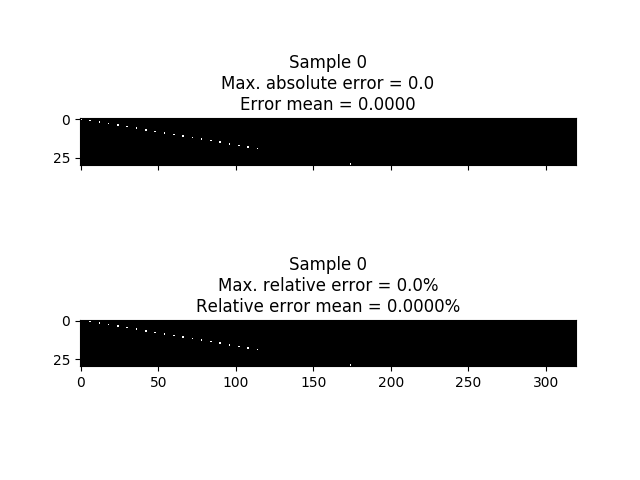
URM Point Frames dataset
As in the functions case, the first thing we must do to train the network for prediction is to resize the data to ensure that the input shape is correct.In this case we must have the following shapes:
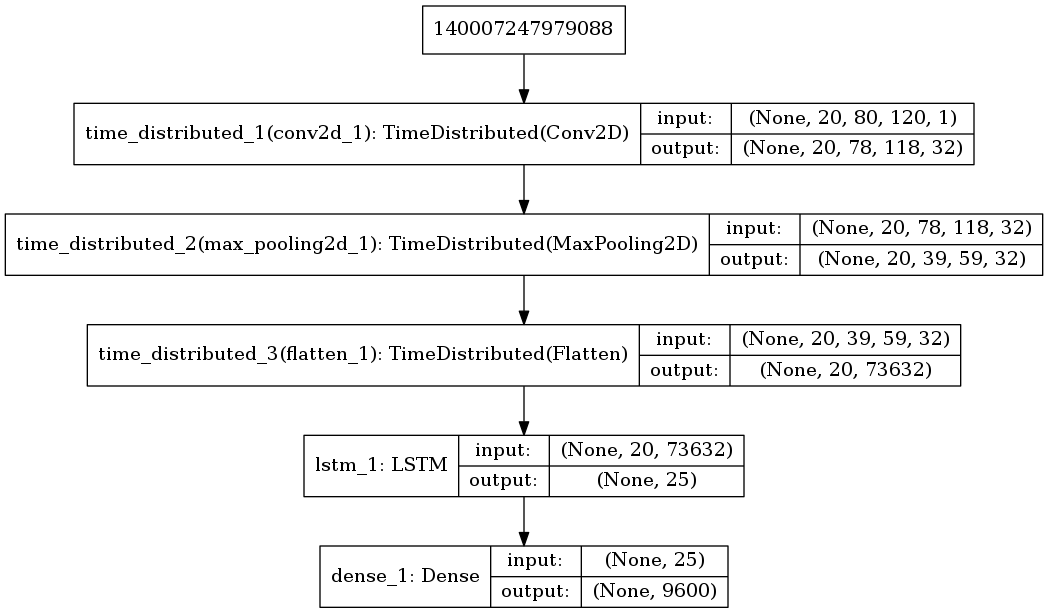
input_shape=(n_samples, know_points=20, height=80, width=120)
output_shape = height * width
For this type of data we have trained 2D convolutional network whose structure can be seen in the following figure:
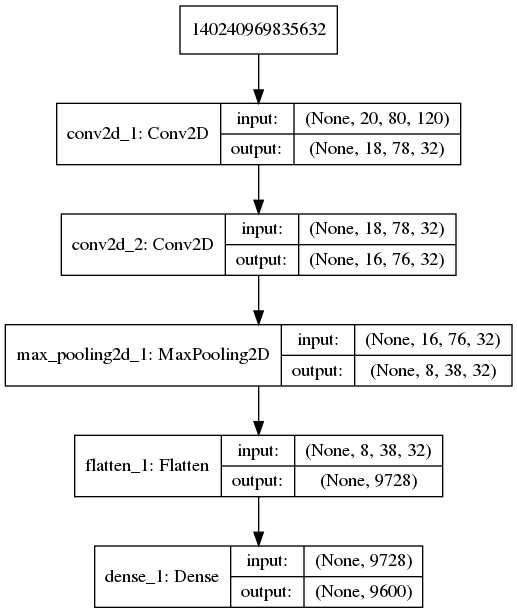
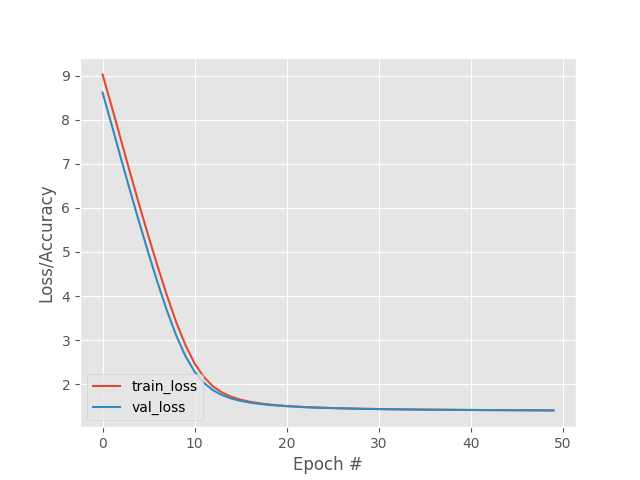
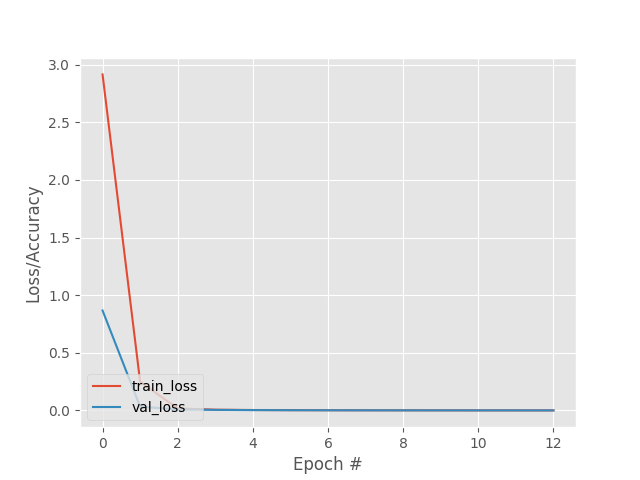
As in the two previous cases, the network manages to reduce and stabilize the loss function in only a few epochs, without any error.
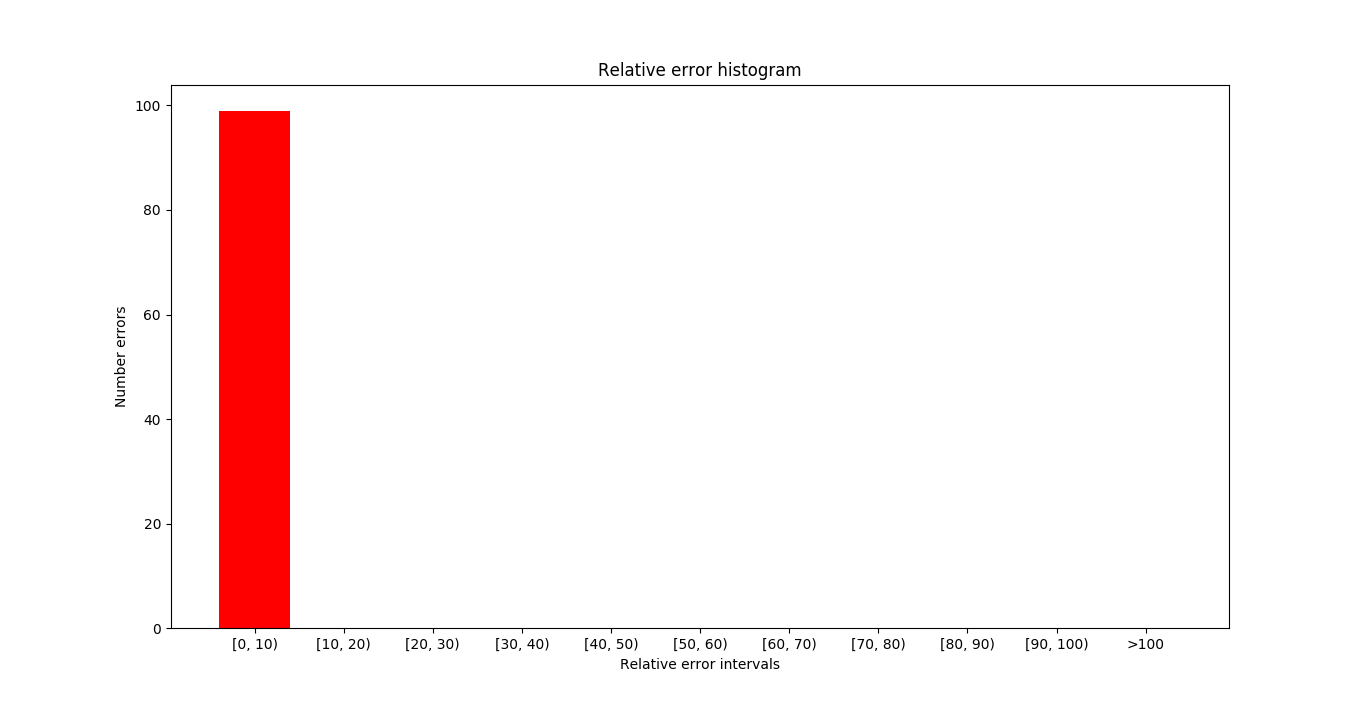
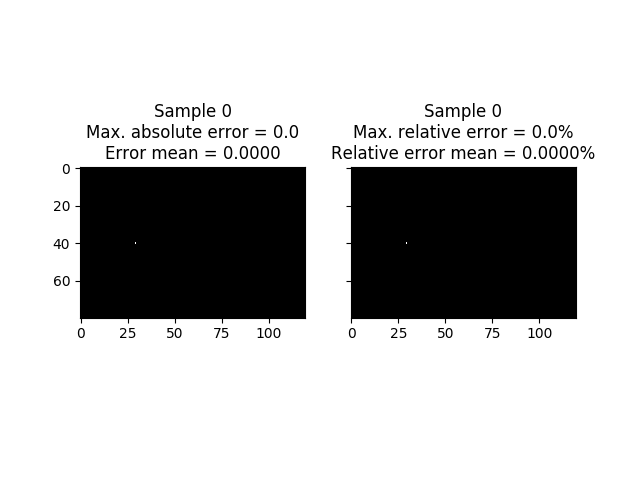
In the next image you can see target frame in the samples where the errors (absolute and relative) are maximum. In this case we have not obtained any error so the first sample is shown.
Training Recurrent Neural Networks - LSTM
Once we have tested the prediction with simple networks without recurrences, we start to train, with the same data, networks that incorporate recurrence. In particular, we will focus the work on the LSTM networks helping us with these tutorials.
Linear Functions dataset
Due to the simplicity of this data and the good result obtained with non-recurrent networks, we have decided not to train recurrent networks with this type of data.
URM Vectors dataset
Although the result with non-recurrent networks was perfect, we decided to use this data to start with the new networks and verify that we have understood their implementation. As in the non-recurrent case, the first thing we must do is to resize the data to ensure that the input shape is correct.nothing changes with respect to non-recurrent networks, so we must have the following shapes:
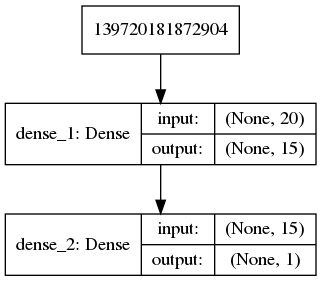
input_shape=(n_samples, know_points=20, vector_length=320)
output_shape = vector_length
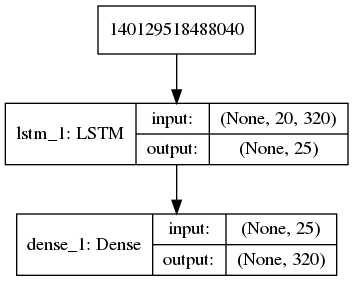
For this type of data we have trained a simple LSTM network whose structure can be seen in the following figure:
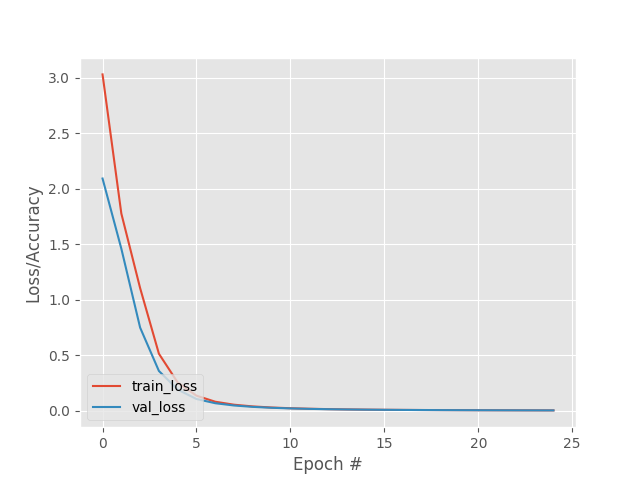
As in the previous case, the network manages to reduce and stabilize the loss function in only a few epochs, without any error.
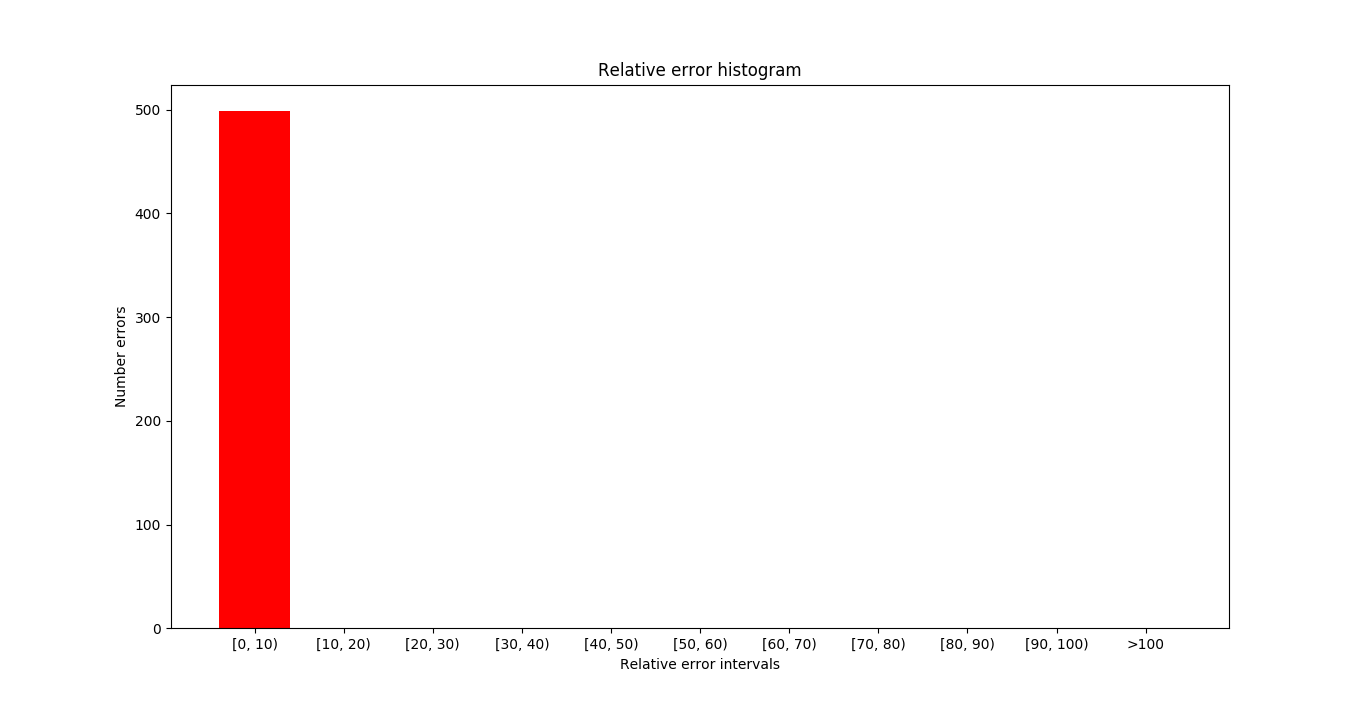
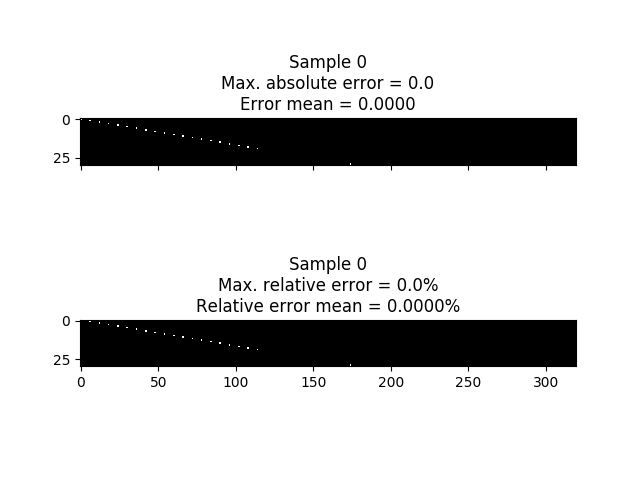
In the next image you can see the samples where the errors (absolute and relative) are maximum. In this case we have not obtained any error so the first sample is shown.
URM Point Frames dataset
For the same reason that in the case of vectors we decided to develop a recurrent network for this type of data, verifying that the implementation we made is correct. In this case we must modify the structure of the data in the following way:
input_shape=(n_samples, know_points=20, height=80, width=120, channels=1)
output_shape = height * width * channels
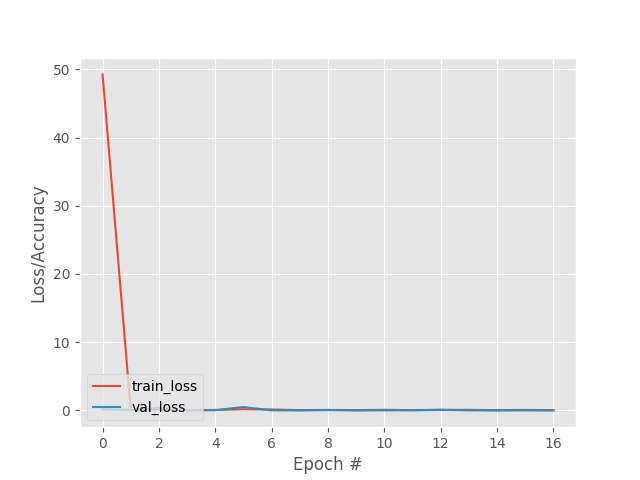
Due to the computational load involved in the training and evaluation of this network it is not yet possible to show the result of the evaluation, although its structure and evolution in training is shown.